译者按
本文为 Yann LeCun 经典论文《A tutorial on energy-based learning》的中文翻译，目标是为了更好的学习这一篇经典著作。
如果需要有更好的阅读体验，也可以阅读本文的 PDF 版本，对排版、翻译的质量问题，可在本文中留言或标记，也可邮件联系本人进行处理：linxuhong@yahoo.com
摘要
基于能量的模型 (EBM) 通过将标量能量与变量的每个配置相关联来捕获变量之间的依赖关系。推理包括限制观察到的变量的值并找到使能量最小化的剩余变量的配置。学习包括找到一个能量函数，其中观察到的变量配置的能量低于未观察到的变量配置。EBM 方法为许多学习模型提供了一个通用的理论框架，包括传统的判别和生成方法，以及图变换器网络、条件随机场、最大边际马尔可夫网络和几种流形学习方法。
概率模型必须经过适当的归一化，有时需要对所有可能的变量配置空间求难以计算的积分。由于 EBM 不需要进行适当的归一化，因此这个问题自然而然地就被规避了。EBM 可以看作是一种非概率因子图，与概率方法相比，它们在架构和训练标准设计方面提供了更大的灵活性。
简介：基于能量的模型
统计建模和机器学习的主要目的是对变量之间的依赖关系进行编码。通过捕获这些依赖关系，可以使用模型来回答有关已知变量值的情况下未知变量值的问题。
基于能量的模型 (EBM) 通过将标量 能量（兼容性度量）与变量的每个配置相关联来捕获依赖关系。推理， 即做出预测或决策，包括设定观察到的变量的值并找到使能量最小化的剩余变量的值。学习包括找到一个能量函数，该函数将低能量与剩余变量的正确值相关联，将高能量与错误值相关联。在学习过程中最小化的损失函数用于衡量可用能量函数的质量。
在这个常见的推理/学习框架内，能量函数和损失函数的广泛选择允许设计多种类型的统计模型，包括概率和非概率的。
基于能量的学习为许多概率和非概率学习方法提供了统一的框架，特别是对于图形模型和其他结构化模型的非概率训练。基于能量的学习可以看作是预测、分类或决策任务的概率估计的替代方案。由于不需要适当的规范化，基于能量的方法避免了与估计概率模型中的规范化常数相关的问题。此外，没有规范化条件使得学习机的设计更加灵活。大多数概率模型可以看作是基于能量的特殊类型的模型，其中能量函数满足某些可规范化条件，并且通过学习优化的损失函数具有特定形式。
本章介绍了基于能量的模型，重点介绍了它们在结构化输出问题和序列标记问题中的应用。第 1 节介绍了基于能量的模型，并描述了通过能量最小化进行确定性推理。第 2 节介绍了基于能量的学习和损失函数的概念。描述了许多标准和非标准损失函数，包括感知器损失、几个基于边际的损失和负对数似然损失。负对数似然损失可用于训练模型以产生条件概率估计。第 3 节展示了如何在 EBM 框架中制定简单的回归和分类模型。第 4 节涉及包含潜在变量的模型。第 5 节详细分析了各种损失函数，并给出了损失函数必须满足的充分条件，以便其最小化将使模型接近所需的行为。给出了“好”和“坏”损失函数的列表。第 6 节介绍了非概率因子图的概念，并非正式地讨论了有效的推理算法。第 7 节重点介绍序列标记和结构化输出模型。在 EBM 框架中重新表述了线性模型，例如最大边际马尔可夫网络和条件随机场。回顾了语音和手写识别的判别学习文献，这些文献可以追溯到 80 年代末和 90 年代初。这包括集成非线性判别函数（例如神经网络）和序列比对方法（例如动态时间规整和隐马尔可夫模型）的全局训练系统。还回顾了分层模型（例如图变换器网络架构）。最后，第 8 节讨论了基于能量的方法、概率方法和基于采样的近似方法（例如对比散度）的差异、共同点和相对优势。
基于能量的推理
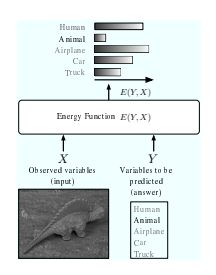
让我们考虑一个包含两组变量 X 和 Y 的模型，如 Figure 1 所示。变量 X 可以是包含对象图像像素的向量。
变量 Y 可以是一个离散变量，表示对象的可能类别。例如，Y 可以取六个可能的值：动物、人体、飞机、卡车、汽车和“以上都不是”。该模型被视为一个能量函数，用于测量 X 和 Y 的每个可能配置的“好坏”。输出数字可以解释为 X 和 Y 值之间的兼容程度。在下文中，我们使用以下惯例：较小的能量值对应于高度兼容的变量配置，而较大的能量值对应于高度不兼容的变量配置。这种类型的函数在不同的技术社区中有不同的名称；它们可能被称为对比函数、值函数或负对数似然函数。在下文中，我们将使用术语能量函数并将其表示为 E (Y, X)。应该区分由推理过程最小化的能量函数和由学习过程最小化的损失函数（第 2 节中介绍）。
在模型最常见的用法中，输入 X 是给定的（从世界观察到的）， 模型得出的答案是与观察到的 X 最相容的 Y。
更准确地说，该模型必须产生从集合 Y 中选择的值 Y *，使得 E ( Y, X ) 最小：
\[Y^{*}=\mathrm{argmin}_{Y\in\mathcal{Y}}E(Y,X). \tag{1}\]
当集合 Y 的大小很小时，我们可以简单地计算 Y ∈ Y 的所有可能值的 E ( Y , X ) 并选取最小的值。
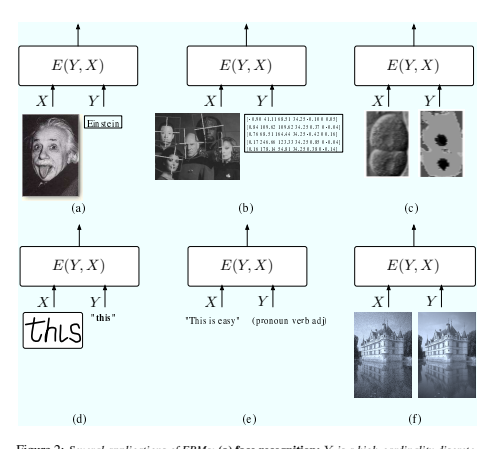
但一般来说，挑选最佳的 Y 可能并不简单。Figure 2 描述了几种 Y 可能太大而无法进行穷举搜索的情况。在@fig-02(a) 中，该模型用于识别人脸。在这种情况下，集合 Y 是离散的和有限的，但其基数可能达到数万 [Chopra et al., 2005]。在@fig-02(b) 中，该模型用于查找图像中的人脸并估计其姿势。集合 Y 包含每个位置的二进制变量，指示该位置是否存在人脸，以及一组表示人脸的大小和方向的连续变量 [Osadchy et al., 2005]。在@fig-02(c) 中，该模型用于分割生物图像：每个像素必须归入五类之一（细胞核、核膜、细胞质、细胞膜、外部介质）。在这种情况下，Y 包含所有 一致 的标签图像，即核膜环绕细胞核、细胞核和细胞质位于细胞壁内等的图像。该集合是离散的，但非常大。更重要的是，集合的成员必须满足复杂的一致性约束 [Ning et al., 2005]。在@fig-02(d) 中， 该模型用于识别手写句子。这里 Y 包含英语的所有可能句子，英语是一组离散但无限的符号序列 [LeCun et al., 1998a]。在@fig-02(f) 中，该模型用于恢复图像（通过清除噪音、增强分辨率或去除划痕）。集合 \(\Nu\) 包含了所有可能的图像（所有可能的像素组合），是一个连续且高维的集合。
对于上述每种情况，都有一个特定的策略，称为“推理程序”， 必须使用 来找到最小化 E(Y, X) 的 Y。在许多实际情况下，推理过程将产生一个近似结果，对于给定的 X，该结果可能是也可能不是 E(Y, X) 的全局最小值。事实上，在某些情况下，E(Y, X) 可能有几个等效最小值。最佳推理过程通常取决于模型的内部结构。例如，如果 Y 是连续的，并且 E(Y, X) 相对于 Y 是平滑且表现良好的，则可以使用基于梯度的优化算法。如果 Y 是离散变量的集合，并且能量函数可以表示为 因子图，即依赖于不同变量子集的能量函数（因子）的总和，则可以使用有效的因子图推理程序（参见第 6 节）[Kschischang 等人，2001 年，MacKay，2003 年]。此类程序的一个流行示例是 最小和 算法。当 Y 的每个元素都可以表示为加权有向无环图中的一条路径时，特定 Y 的能量就是特定路径上边和节点的值之和。在这种情况下，可以使用动态规划（例如使用 Viterbi 算法或 A∗）有效地找到最佳 Y。这种情况通常发生在序列标记问题中，例如语音识别、手写识别、自然语言处理和生物序列分析（例如基因查找、蛋白质折叠预测等）。不同情况可能需要使用其他优化程序，包括连续优化方法（例如线性规划、二次规划、非线性优化方法）或离散优化方法（例如模拟退火、图切割或图匹配）。在许多情况下，精确优化是不切实际的，必须求助于近似方法，包括使用替代能量函数的方法（例如变分方法）。
模型可以回答什么问题？
在前面的讨论中，我们暗示模型要回答的问题是“与这个 X 最兼容的 Y 是什么？”，这种情况发生在预测、分类或决策任务中。然而，模型可以用来回答几种类型的问题：
预测、分类和决策：“哪个 Y 值与这个 X 最兼容？”这种情况发生在使用模型进行艰难决策或产生动作时。例如，如果使用模型来驱动机器人并避开障碍物，它必须产生一个最佳决策，例如“左转”、“右转”或“直行”。
排序：“Y1 还是 Y2 与这个 X 更兼容？”这是一项比分类更复杂的任务，因为必须训练系统对所有答案进行完整的排序，而不是仅仅产生最佳答案。这种情况发生在许多数据挖掘应用中，其中模型用于选择最符合给定标准的多个样本。
检测：“这个 Y 值与 X 兼容吗？”通常，检测任务（例如检测图像中的脸部）是通过将脸部标签的能量与阈值进行比较来执行的。由于在构建系统时阈值通常是未知的，因此必须对系统进行训练，使其产生能量值，当图像看起来不像脸部时，能量值会增加。
条件密度估计：“给定X，Y的条件概率分布是多少？”这种情况发生在系统的输出不直接用于产生动作，而是提供给人类决策者或馈送到另一个单独构建的系统的输入时。 我们经常将 X 视为高维变量（例如图像），将 Y 视为离散变量（例如标签），但相反的情况也很常见。当模型用于图像恢复、计算机图形学、语音和语言生成等应用时，就会发生这种情况。最复杂的情况是 X 和 Y 都 是高维的。
决策与概率建模
对于决策任务（例如操纵机器人），系统只需将最低能量分配给正确答案即可。其他答案的能量无关紧要，只要它们更大即可。但是，系统的输出有时必须与另一个系统的输出相结合，或馈送到另一个系统的输入（或馈送到人类决策者）。由于能量未校准（即以任意单位测量），因此将两个单独训练的基于能量的模型结合起来并不简单： 没有先验保证它们的能量尺度是相称的。校准能量以允许这种组合可以通过多种方式完成。但是，唯一一致的方法是将所有可能输出的能量集合转换为归一化概率分布。将任意能量集合转换为 0 到 1 之间的数字集合（其总和（或积分）为 1）的最简单和最常见的方法是通过吉布斯分布：
\[P(Y|X)={\frac{e^{-\beta E(Y,X)}}{\int_{y\in{\mathcal{Y}}}e^{-\beta E(y,X)}}}, \tag{2}\]
其中 \(\beta\) 是一个任意的正常数，类似于温度的倒数，分母称为 分配函数（与统计物理学中的类似概念类似）。选择 Gibbs 分布可能看起来是任意的，但可以通过适当重新定义能量函数来获得（或近似）其他概率分布。以这种方式获得的数字是否是好的概率估计并不取决于能量如何转化为概率，而取决于如何从数据中估计 \(E(Y, X)\)。
需要注意的是，上述将能量转换为概率的方法只有在积分 \(\int_{y\in\mathcal{Y}}e^{-\beta E(y,X)}\) 收敛时才有可能。这在一定程度上限制了可以使用的能量函数和域 Y。更重要的是，在许多实际情况下，计算分区函数是难以处理的（例如当 Y 具有高基数时），或者完全不可能（例如当 Y 是高维变量并且积分没有解析解时）。因此，概率建模的代价很高，当应用程序不需要它时应该避免使用。
基于能量的训练：架构和损失函数
训练 EBM 就是找到一个能量函数，该函数能为任意 X 产生最佳 Y。最佳能量函数的搜索是在由参数 W 索引的能量函数族 E 中进行的
\[ \mathcal{E}=\{E(W,Y,X):W\in\mathcal{W}\}。 \]
EBM 的 架构 是参数化能量函数 \(E(W, Y, X)\) 的内部结构。此时，我们对 X、Y、W 和 E 的性质没有特别的限制。当 X 和 Y 是实向量时，E 可以简单到只是基函数的线性组合（如核方法的情况），或者一组神经网络架构和权重值。本节给出了分类和回归常见应用的简单架构示例。当 X 和 Y 是可变大小的图像、符号或向量序列或更复杂的结构化对象时，E 可能代表一类相当丰富的函数。第 4、6 和 7 节讨论了此类架构的几个示例。基于能量的方法的一个优点是它对 \(\varepsilon\) 的性质几乎没有限制。
为了训练模型进行预测、分类或决策，我们给出了一组训练样本 \(\mathcal{S}=\{(X^{i},Y^{i}):i=1\ldots P\}\)，其中 \(X^{i}\) 是第 \(\text{i-th}\) 个训练样本的输入，\(\text{Yi}\) 是相应的期望答案。为了在 E 族中找到最佳能量函数，我们需要一种方法来评估任何
特定的能量函数，仅基于两个元素：训练集和我们对任务的先验知识。这个质量指标称为“损失函数”（即 函数的函数）并表示为 L(E, S)。为简单起见，我们经常将其表示为 L(W, S)，并简称为“损失函数”。学习问题只是找到 W， 尽量减少损失：
\[W^{*}=\operatorname*{min}_{W\in{\mathcal{W}}}{\mathcal{L}}(W,{\mathcal{S}})。 \tag{3}\]
大多数情况下，损失函数定义如下：
\[{\cal L}(E,{\cal S})=\frac{1}{P}\sum_{i=1}^{P}L(Y^{i},E(W,{\cal Y},X^{i}))+R(W)。 \tag{4}\]
它是对训练集取的每个样本损失函数的平均值，表示为 \(L(Y^{i},E(W,\mathcal{Y},X^{i}))\)，它取决于所需的答案 \(Y^i\) 以及通过保持输入样本固定并改变答案 \(Y\) 获得的能量。因此，对于每个样本，我们评估能量表面的“切片”。术语 \(R(W)\) 是正则化器， 并可用于嵌入我们关于哪些能量函数在我们的家族中优于其他函数的先验知识（在没有训练数据的情况下）。根据此定义，损失在训练样本的排列和训练集的多次重复下保持不变。
当然，学习的最终目的是生成一个模型，该模型将为训练期间未见过的新输入样本提供良好的答案。我们可以依靠统计学习理论的一般结果，该理论保证，在样本的简单可互换性条件下以及能量函数族（有限 VC 维）的一般条件下，训练集上的损失值在最小化后与一组大型独立测试样本上的损失之间的偏差受一个数量的限制，该数量随着训练集的大小增加而收敛到零 [Vapnik，1995]。
设计损失函数
直观地讲，每个样本的损失函数应该这样设计：将低损失分配给表现良好的能量函数：将最低能量分配给正确答案，将较高能量分配给所有其他（错误）答案的能量函数。相反，没有将最低能量分配给正确答案的能量函数将产生高损失。以下章节将进一步讨论损失函数（选择最佳能量函数的函数）的适当性。
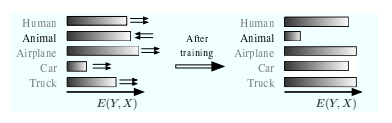
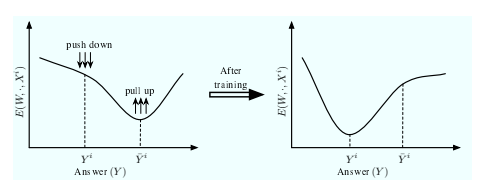
仅考虑训练模型以回答第 1 类问题（预测、分类和决策）的任务，基于能量的方法的主要直觉如下。训练 EBM 包括塑造能量函数，以便对于任何给定的 X，推理算法都会产生 Y 的期望值。由于推理算法选择具有最低能量的 Y，因此学习过程必须塑造能量表面，以使 Y 的期望值具有低于所有其他（不期望）值的能量。图 3 和图 4 显示了能量作为 Y 函数的示例 对于给定的输入样本 Xi，在 Y 为离散变量和连续标量变量的情况下。我们注意到三种类型的答案：
- \(Y^i\)：正确答案
- \(Y^{∗i}\)：模型产生的答案，即能量最低的答案。
- \(\bar{Y}^i\)：最令人反感的错误答案，即所有错误答案中能量最低的答案。要在连续情况下定义此答案，我们可以简单地将距离 \(Y^i\) 为 ǫ 内的所有答案视为正确答案，将距离 \(Y^i\) 以外的所有答案视为错误答案。
如果损失函数设计得当，学习过程应该具有“下推”\(E(W,Y^i,X^i)\) 和“上拉”不正确能量（尤其是 \(E(W,\bar{Y}^{i},X^{i})\)）的效果。不同的损失函数以不同的方式实现这一点。第 5 节给出了损失函数必须满足的充分条件，以保证正确地塑造能量表面。我们表明，一些广泛使用的损失函数不满足条件，而其他损失函数则满足条件。
总结一下：给定一个训练集 S，构建和训练基于能量的模型涉及设计四个组件：
架构：\(E(W, Y, X)\)的内部结构。
推理算法：对于给定的 X，寻找使得 \(E(W, Y, X)\) 最小化的 Y 值的方法。
损失函数：L(W, S) 使用训练集来测量能量函数的质量。
学习算法：在给定训练集的情况下，寻找一个最小化能量函数族\(\varepsilon\)上的损失函数的W 的方法。
正确设计架构和损失函数至关重要。我们可能对手头任务的任何先验知识都嵌入到架构和损失函数（特别是正则化器）中。不幸的是，并非所有架构和损失函数的组合都是允许的。对于某些组合，最小化损失不会使模型产生最佳答案。选择能够有效和高效学习的架构和损失函数组合对于基于能量的方法至关重要，因此是本教程的中心主题。
损失函数示例
现在，我们来描述机器学习文献中提出并使用的一些标准损失函数。我们将讨论这些函数，并在基于能量的设置中将它们归类为“好”或“坏”。暂时，我们先将正则化项放在一边，集中讨论损失函数中与数据相关的部分。
能量损失
所有损失函数中最简单、最直接的是能量损失。
对于训练样本（Xi，Yi），每个样本的损失定义简单为：
\[L_{能量}(Y^{i},E(W,\mathcal{Y},X^{i}))=E(W,Y^{i},X^{i})。 \tag{5}\]
虽然这种损失函数在回归和神经网络训练等方面非常流行，但它不能用于训练大多数架构：虽然这种损失会降低所需答案的能量，但不会提高任何其他能量。对于某些架构，这可能导致能量恒定且等于零的崩溃解决方案。能量损失只适用于这样一种架构：降低 \(E(\tilde{W},Y^{i},X^{i})\) 会自动使其他答案的能量变大。这种架构的一个简单示例是 \(E(W,Y^{i},X^{i})=||Y^{i}-G(W,X^{i})||^{2}\)，它对应于以 \(G\) 为回归函数的均方误差回归。
广义感知器损失
训练样本（Xi，Yi）的广义感知器损失定义为
\[L_{感知器}(Y^{i},E(W,{\cal Y},X^{i}))=E(W,Y^{i},X^{i})-\min_{Y\in{\cal Y}}E(W,Y,X^{i})。 \tag{6}\]
这个损失总是正的，因为第二项是第一项的下限。
最小化这种损失会降低 E(W, Y i, Xi)，同时提高模型产生的答案的能量。
虽然感知器损失已广泛应用于许多领域，包括具有结构化输出的模型，例如手写识别 [LeCun et al., 1998a] 和词性标注 [Collins, 2002]，它有一个重大缺陷：没有在正确答案和错误答案之间创建能量间隙的机制。
因此，与能量损失一样，如果架构允许，感知器损失可能会产生平坦（或几乎平坦）的能量表面。因此，只有使用无法产生平坦能量表面的模型时，才能保证这种损失产生有意义的、未坍缩的结果。对于其他模型，无法保证任何事情。
广义保证金损失
有几种损失函数可以描述为边际损失；铰链损失、对数损失、LVQ2 损失、最小分类误差损失、平方平方损失和平方指数损失都使用某种形式的边际来在正确答案和错误答案之间创建能量差距。在讨论广义边际损失之前，我们给出以下定义。
定义 1 假设 Y 为离散变量。那么对于训练样本 (Xi, Y i)，最令人讨厌的错误答案 Y¯ i*是所有错误答案中能量最低的答案：
\[\bar{Y}^{i}=\mathrm{argmin}_{Y\in\mathcal{Y}andY\neq Y^{i}}E(W,Y,X^{i})。 \tag{7}\]
如果Y是连续变量，那么最令人反感的错误答案可以用多种方式定义。最简单的定义如下。
定义 2 假设 Y 是一个连续变量。那么对于训练样本 (Xi, Y i)，最令人反感的错误答案 Y¯ i 是所有距离正确答案至少为 ǫ 的答案中能量最低的答案：
\[\bar{Y}^{i}=\mathrm{argmin}_{Y\in\mathcal{Y},\|Y-Y^{i}\|>\epsilon}E(W,Y,X^{我}). \tag{8}\]
广义边际损失是广义感知器损失的更稳健版本。它直接使用对比项中最令人反感的错误答案的能量：
\[L_{\mathrm{margin}}(W,Y^i,X^i)=Q_m\left(E(W,Y^i,X^i),E(W,\bar{Y}^i,X^i)\right)。 \tag{9}\]
这里 m 是一个正参数，称为 margin，Qm(e1, e2) 是一个凸函数，其梯度在 E(W, Y i, Xi)+m > E(W, Y¯ i, Xi) 的区域中与向量 [1, −1] 具有正点积。换句话说，只要 E(W, Y i, Xi) 不小于 E(W, Y¯ i, Xi) 至少 m，损失表面就会向 E(W, Y i, Xi) 的低值和 E(W, Y¯ i, Xi) 的高值倾斜。下面给出了广义边缘损失的两种特殊情况： 铰链损失：广义边缘损失的一个特别流行的例子是铰链损失，它与线性参数化能量和支持向量机、支持向量马尔可夫模型 [Altun and Hofmann, 2003] 和最大边缘马尔可夫网络 [Taskar et al., 2003] 中的二次正则化器结合使用：
\[L_{\mathrm{hinge}}(W,Y^i,X^i)=\max\left(0,m+E(W,Y^i,X^i)-E(W,\bar{Y}^i,X^i)\right), \tag{10}\]
其中 m 是正边距。此损失函数的形状在@fig-05 中给出。当正确答案和最令人反感的错误答案的能量差大于 −m 时，将受到线性惩罚。铰链损失仅取决于能量差异，因此单个能量不受任何特定值的限制。
对数损失：铰链损失的一个常见变体是对数损失，它可以看作是具有无限边距的铰链损失的“软”版本（参见@fig-05，中心）：
\[L_{\log}(W,Y^{i},X^{i})=\log\left(1+e^{E(W,Y^{i},X^{i})-E(W,\bar{Y}^{i},X^{i})}\right). \tag{11}\]
LVQ2 损失：最早用于判别训练序列标记系统（特别是语音识别系统）的提案之一 是 Kohonen 的 LVQ2 损失的一个版本。自 20 世纪 90 年代初以来，Driancourt 和 Bottou 就一直提倡这种损失 [Driancourt et al., 1991a, Driancourt and Gallinari, 1992b, Driancourt and Gallinari, 1992a, Driancourt, 1994, McDermott, 1997, McDermott and Katagiri, 1992]：
\[L_{\rm lvq2}(W,Y^{i},X^{i})=\min\left(1,\max\left(0,\frac{E(W,Y^{i},X^{i})-E(W,\bar{Y}^{i},X^{i})}{\delta E(W,Y^{i},X^{i})}\right)\right), \tag{12}\]
其中 \(\delta\) 是正参数。LVQ2 是零边际损失，但它具有将 \(E(W,Y^{i},X^{i})\) 和 \(E(\bar{W},\bar{Y}^{i},X^{i})\) 之间的比率饱和到 \(1 + \delta\) 的特性。这通过使异常值对总损失贡献名义成本 M 来减轻异常值的影响。
该损失函数是对分类错误数量的连续近似。
与广义边缘损失不同，LVQ2 损失在 \(E(W,Y^{i},X^{i})\) 和 \(E(\bar{W},\bar{Y}^{i},X^{i})\) 中是非凸的。
MCE 损失：最小分类错误损失最初由 Juang 等人在语音识别系统的判别训练背景下提出 [Juang et al., 1997]。其动机是构建一个损失函数，该函数还可以近似地计算分类错误的数量，同时保持平滑和可微分。分类错误的数量可以写成：
\[\theta\left(E(W,Y^i,X^i)-E(W,\bar{Y}^i,X^i)\right), \tag{13}\]
其中 θ 是阶跃函数（负参数为零，正参数为 1）。但是，此函数不可微，因此很难优化。MCE 损失使用 S 形函数“软化”它：
\[L_{\mathrm{mce}}(W,Y^i,X^i)=\sigma\left(E(W,Y^i,X^i)-E(W,\bar{Y}^i,X^i)\right), \tag{14}\]
其中 \(\sigma\) 是逻辑函数 \(\sigma(x)=(1+e^{-x})^{-1}\)。与 LVQ2 损失一样，饱和度确保错误对整体损失的贡献很小。虽然 MCE 损失没有明确的余量，但它确实在 \(E(W,Y^{\bar{i}},X^{i})\) 和 \(E(W,\bar{Y}^{i},X^{i})\) 之间产生了差距。MCE 损失是非凸的。
Square-Square 损失：与 hinge 损失不同，square-square 损失将正确答案和最有问题的答案的能量分开处理 [LeCun and Huang, 2005, Hadsell et al., 2006]：
\[L_{sq-\exp}(W,Y^{i},X^{i}) = E(W,Y^{i},X^{i})^{2}+\left(\max(0,m-E(W,\bar{Y}^{i},X^{i}))\right)^{2}. \tag{15}\]
边界 m 以下的 \(E(W,Y^i,X^i)\) 的较大值和 \(E(W,\bar{Y}^{i},X^{i})\) 的较小值均会受到二次惩罚（参见@fig-05）。与边界损失不同，squaresquare 损失将正确答案能量“限制”在零，将错误答案能量“限制”在 m 以上。因此，它仅适用于低于零的能量函数，尤其是在输出模块测量某种距离的架构中。
平方指数 [LeCun 和 Huang，2005 年，Chopra 等人，2005 年，Osadchy 等人，2005 年]：平方指数损失与平方平方损失类似。两者的区别仅在于对比项：它不是二次项，而是最令人反感的错误答案的负能量的指数：
\[ L_{sq-\exp}(W,Y^{i},X^{i})=E(W,Y^{i},X^{i})^{2}+\gamma e^{-E(W,\overline{Y}^{i},X^{i})}， \tag{16}\]
其中 γ 是正常数。与平方损失不同，该损失具有无限的余量，并以指数递减的力量将错误答案的能量推向无穷大。
负对数似然损失
负对数似然损失的动机来自概率建模。它定义为：
\[L_{\mathrm{null}}(W,Y^{i},X^{i})=E(W,Y^{i},X^{i})+{\mathcal{F}}_{\beta}(W,{\mathcal{Y}},X^{i})。 \tag{17}\]
其中 F 是集合 {E(W, y, Xi), y ∈ Y} 的 自由能：
\[{\cal F}_{\beta}(W,{\cal Y},X^{i})=\frac{1}{\beta}\log\left(\int_{y\in{\cal Y}}\exp\left(-\beta E(W,y,X^{i})\right)\right)。 \tag{18}\]
其中 \(\beta\) 是一个类似于温度倒数的正常数。只有当负能量的指数在 Y 上可积时，才能使用此损失，而对于某些能量函数或 Y 的选择，情况可能并非如此。
负对数似然损失的形式源于根据最大条件概率原理对学习问题的概率公式化。
给定训练集 S，我们必须找到一个参数值，该参数值使得在给定训练集中所有输入的情况下，所有答案的条件概率最大化。假设样本是独立的，用 \(P(Y^{i}|X^{i},W)\) 表示给定 \(X^i\) 时 \(Y^i\) 的条件概率，该概率由我们的模型以参数 \(W\) 生成，则该模型下训练集的条件概率是样本的简单乘积：
\[P(Y^{1},\ldots,Y^{P}|X^{1},\ldots,X^{P},W)=\prod_{i=1}^{P}P(Y^{i}|X^{i},W)。 \tag{19}\]
应用最大似然估计原理，我们寻求使上述乘积最大化的 W 值，或者使上述乘积的负对数最小化的 W 值：
\[-\log\prod_{i=1}^{P}P(Y^{i}|X^{i},W)=\sum_{i=1}^{P}-\log P(Y^{i}|X^{i},W)。 \tag{20}\]
使用吉布斯分布（公式 2），我们得到：
\[-\log\prod_{i=1}^{P}P(Y^{i}|X^{i},W)=\sum_{i=1}^{P}\beta E(W,Y^{i},X^{i})+\log\int_{y\in\mathcal{Y}}e^{-\beta E(W,y,X^{i})}. \tag{21}\]
负对数似然损失的最终形式是通过将上述表达式除以 P 和 β（对最小值的位置没有影响）得到的：
\[{\mathcal{L}}_{\mathrm{null}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\left(E(W,Y^{i},X^{i})+{\frac{1}{\beta}}\log\int_{y\in{\mathcal{Y}}}e^{-\beta E(W,y,X^{i})}\right). \tag{22}\]
虽然许多先前的损失函数在其对比项中仅涉及 E(W, Y¯ i, Xi)，但负对数似然损失在其对比项 Fβ(W, Y, Xi) 中结合了 Y 所有值的所有能量。该项可以解释为能量为 E(W, Y, Xi) 的系统集合的亥姆霍兹自由能（对数分区函数），Y ∈ Y。这个对比项导致所有答案的能量被拉高。正确答案的能量也被拉高，但没有第一个项向下推的那么厉害。这可以在单个样本的梯度表达式中看到：
\[\frac{\partial L_{\rm{null}}(W,Y^{i},X^{i})}{\partial W}=\frac{\partial E(W,Y^{i},X^{i})}{\partial W}-\int_{Y\in\mathcal{Y}}\frac{\partial E(W,Y,X^{i})}{\partial W}P(Y|X^{i},W), \tag{23}\]
其中 \(P(Y|X^{i},W)\) 是通过 Gibbs 分布获得的：
\[P(Y|X^{i},W)=\frac{e^{-\beta E(W,Y,X^{i})}}{\int_{y\in\mathcal{Y}}e^{-\beta E(W,y,X^{i})}}. \tag{24}\]
因此，对比项会以与该答案在模型下出现的可能性成比例的力量来提升每个答案的能量。不幸的是，有许多有趣的模型，计算 \(\gamma\) 上的积分是难以解决的。评估这个积分是一个主要的研究课题。人们已经投入了大量精力来研究近似方法，包括巧妙地组织计算、蒙特卡罗采样方法和变分方法。虽然这些方法被设计为最小化 NLL 损失的近似方法，但它们可以在基于能量的框架中被视为选择将提升其能量的 Y 的不同策略。
有趣的是，当 \(\beta\rightarrow\infty\)（零温度）时，NLL 损失减少为广义感知器损失，而当 \(\gamma\) 有两个元素（例如二元分类）时，NLL 损失减少为对数损失 Equation 11。
许多作者以各种名称广泛使用了 NLL 损失。在神经网络分类文献中，它被称为 交叉熵损失 [Solla 等人，1988]。Bengio 等人还使用它来训练基于能量的语言模型 [Bengio 等人，2003]。自 80 年代末以来，它一直以 最大互信息估计 的名称广泛用于有区别地训练语音识别系统，包括混合高斯的隐马尔可夫模型 [Bahl 等人，1986] 和 HMM-神经网络混合模型 [Bengio 等人，1990，Bengio 等人，1992，Haffner，1993，Bengio，1996]。它还被广泛用于集成神经网络和隐马尔可夫模型的手写识别系统的全局判别训练，其名称为最大互信息 [Bengio et al., 1993, LeCun and Bengio, 1994, Bengio et al., 1995, LeCun et al., 1997, Bottou et al., 1997] 和 判别前向训练 [LeCun et al., 1998a]。最后，它是训练其他概率判别序列标记模型的首选损失函数，例如输入/输出 HMM [Bengio and Frasconi, 1996]、条件随机场 [Lafferty et al., 2001] 和判别随机场 [Kumar and Hebert, 2004]。
最小经验误差损失：一些作者认为，负对数似然损失过于强调错误：等式 20 是一个乘积，其值由其最小项决定。因此，Ljolje 等人 [Ljolje et al., 1990] 提出了 最小经验误差损失，它将样本的条件概率以加法而不是乘法的方式组合在一起：
\[L_{\mathrm{mee}}(W,Y^{i},X^{i})=1-P(Y^{i}|X^{i},W)。 \tag{25}\]
代入@eq-02 我们得到：
\[L_{\rm mee}(W,Y^{i},X^{i})=1-\frac{e^{-\beta E(W,Y^{i},X^{i})}}{\int_{y\in\mathcal{Y}}e^{-\beta E(W,y,X^{i})}}. \tag{26}\]
与 MCE 损失和 LVQ2 损失一样，MEE 损失使任何单个误差的贡献饱和。这使得系统对标记噪声和异常值更具鲁棒性，这对于语音识别等应用尤为重要，但它使损失非凸。与 NLL 损失一样，MEE 需要评估分区函数。
简单的架构
为了证实迄今为止提出的想法，本节演示了如何将简单的分类和回归模型公式化为基于能量的模型。这为讨论好的和坏的损失函数以及讨论结构化预测的高级架构奠定了基础。
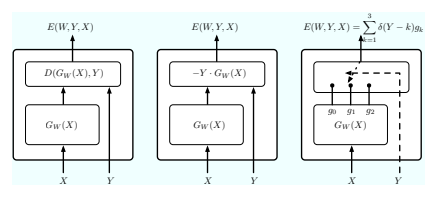
回归
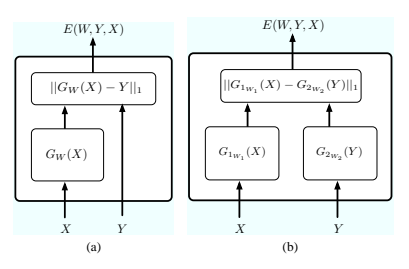
Figure 6(a) 展示了回归或函数逼近的简单架构。能量函数是回归函数 GW (X) 的输出之间的平方误差 以及要预测的变量 Y ，它可以是标量或向量：
\[E(W,Y,X)={\frac{1}{2}}||G_{W}(X)-Y||^{2}. \tag{27}\]
推理问题很简单：最小化 E 的 Y 值等于 GW (X)。
最小能量始终等于零。当使用此架构时，能量损失、感知器损失和负对数似然损失都是等效的，因为感知器损失的对比项为零，而 NLL 损失的对比项为常数（它是方差为常数的高斯积分）：
\[{\mathcal{L}}_{\mathrm{energy}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}E(W,Y^{i},X^{i})={\frac{1}{2P}}\sum_{i=1}^{P}||G_{W}(X^{i})-Y^{i}||^{2}. \tag{28}\]
这对应于具有均方误差的标准回归。
当 G 是参数的线性函数时，就会出现一种流行的回归形式：
\[G_{W}(X)=\sum_{k=1}^{N}w_{k}\phi_{k}(X)=W^{T}\Phi(X). \tag{29}\]
\(\phi_{k}(X)\) 是一组 \(N\) 个 特征，而 \(w_k\) 是 N 维参数向量 W 的分量。为简洁起见，我们使用向量符号 \(W^{T}\Phi(X)\)，其中 \(W^T\) 表示 \(W\) 的转置，而 \(\Phi(X)\) 表示由每个 \(\phi_{k}(X)\) 形成的向量。通过这种线性参数化，使用能量损失进行训练可以简化为易于解决的最小二乘最小化问题，该问题为凸问题：
\[W^{*}=\mathrm{argmin}_{W}\left[\frac{1}{2P}\sum_{i=1}^{P}||W^{T}\Phi(X^{i})-Y^{i}||^{2}\right]. \tag{30}\]
在简单模型中，特征函数由设计者手工设计，或从无标签数据中单独训练。在核方法的对偶形式中，它们被定义为 \(\phi_{k}(X)=K(X,X^{k}),k=1\ldots P\)，其中 \(K\) 是核函数。在更复杂的模型（例如多层神经网络等）中，\(\phi\) 本身可能被参数化并受学习影响，在这种情况下，回归函数不再是参数的线性函数，因此损失函数可能不是参数的凸函数。
二分类器
Figure 6(b) 展示了一个简单的二分类器架构。要预测的变量是二进制的：Y = {−1, +1}。能量函数可以定义为：
\[E(W,Y,X)=-Y G_{W}(X), \tag{31}\]
其中 \(G_{W}(X)\) 是一个标量值 判别函数，由 W 参数化。推理很简单：
\[Y^*=\mathrm{argmin}_{Y\in\{-1,1\}}-YG_W(X)=\mathrm{sign}(G_W(X)). \tag{32}\]
可以使用多种不同的损失函数进行学习，其中包括感知器损失、铰链损失和负对数似然损失。将公式 32 和 33 代入感知器损失（公式 7），我们得到：
\[{\mathcal{L}}_{\mathrm{感知器}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\left(\mathrm{sign}(G_{W}(X^{i}))-Y^{i}\right)G_{W}(X^{i})。 \tag{33}\]
用于最小化该损失的随机梯度下降更新规则是：
\[W\gets W+\eta\left(Y^{i}-\mathrm{sign}(G_{W}(X^{i})\right)\frac{\partial G_{W}(X^{i})}{\partial W}, \tag{34}\]
其中η 是正步长。如果我们选择线性模型系列中的 GW (X)，则能量函数变为 E(W, Y, X) = −Y WT Φ(X)，感知器损失变为：
\[{\mathcal{L}}_{\mathrm{感知器}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\left(\mathrm{sign}(W^{T}\Phi(X^{i}))-Y^{i}\right)W^{T}\Phi(X^{i}), \tag{35}\]
随机梯度下降更新规则变成了我们熟悉的感知器学习规则：W ← W + ηY i − sign(WT Φ(Xi))Φ(Xi)。
铰链损失 (Equation 10) 与二分类器能量 (Equation 31) 的乘积为：
\[{\mathcal{L}}_{\mathrm{hinge}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\operatorname*{max}(0,m+2Y^{i}G_{W}(X^{i})). \tag{36}\]
使用该损失与 GW (X) = WT X 以及形式为 ||W||2 的正则化器可得到熟悉的线性支持向量机。
使用公式 32 的负对数似然损失 (Equation 22) 得出：
\[{\mathcal{L}}_{\mathrm{null}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\left[-Y^{i}G_{W}(X^{i})+\log\left(e^{Y^{i}G_{W}(X^{i})}+e^{-Y^{i}G_{W}(X^{i})}\right)\right]. \tag{37}\]
利用事实\(\mathcal{Y}=\{-1,+1\}\)，我们得到：。 \[{\mathcal{L}}_{\mathrm{null}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\log\left(1+e^{-2Y^{i}G_{W}(X^{i})}\right), \tag{38}\]
这相当于对数损失（等式 12）。使用如上所述的线性模型，损失函数变为：
\[{\mathcal{L}}_{\mathrm{null}}(W,{\mathcal{S}})={\frac{1}{P}}\sum_{i=1}^{P}\log\left(1+e^{-2Y^{i}W^{T}\Phi(X^{i})}\right). \tag{39}\]
这种特殊的架构和损失组合就是我们熟悉的逻辑回归方法。
多类分类器
Figure 6(c) 展示了 3 个类别的多类分类架构示例。
判别函数 GW (X) 产生一个输出向量 [g1, g2, . . . , gC]，其中每个 C 类别都有一个分量。每个分量 gj 可以解释为将 X 分配给第 j 个类别的“惩罚”。离散开关模块选择哪个分量连接到输出能量。开关的位置由离散变量 Y ∈ {1, 2, . . . , C} 控制，该变量被解释为类别。输出能量等于 E(W, Y, X) = PC j=1 δ(Y − j)gj ，其中 δ(Y − j) 是克罗内克 δ 函数：当 u = 0 时，δ(u) = 1；否则，δ(u) = 0。
推理在于将 Y 设置为 GW (X) 最小组成部分的索引。
感知器损失、铰链损失和负对数似然损失可以直接转化为多类情况。
隐式回归
上一节中描述的架构是 Y 的简单函数，在 Y 集合中只有一个最小值。但是，有些任务的多个答案同样好用。例如，机器人导航，左转或右转可以同样好地绕过障碍物，或者语言模型，其中句子片段“猫吃了”可以同样好地跟在“老鼠”或“鸟”后面。
更一般地，X 和 Y 之间的依赖关系有时不能表示为将 X 映射到 Y 的函数（例如，考虑约束 X2+Y 2 = 1)。在这种情况下，我们称之为隐式回归，我们模拟 X 和 Y 必须满足的约束，并设计能量函数来衡量对约束的违反。
X 和 Y 都可以通过函数传递，能量是其输出的函数。一个简单的例子是：
\[E(W,Y,X)=\frac{1}{2}||G_{X}(W_{X},X)-G_{Y}(W_{Y},Y)||^{2}. \tag{40}\]
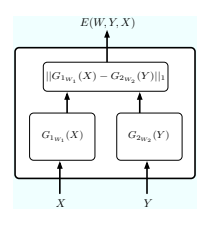
对于某些问题，函数 GX 必须不同于函数 GY 。在其他情况下，GX 和 GY 必须是同一函数 G 的实例。一个有趣的例子是 Siamese 架构 [Bromley et al., 1993]：变量 X1 和 X2 通过函数 GW 的两个实例传递。二进制标签 Y 确定对 GW (X1) 和 GW (X2) 的约束：如果 Y = 0，则 GW (X1) 和 GW (X2) 应该相等，如果 Y = 1，则 GW (X1) 和 GW (X2) 应该不同。这样，对 X1 和 X2 的回归是通过约束 Y 隐式学习的，而不是通过监督明确学习的。Siamese 架构用于学习带有标记示例的相似性度量。当已知两个输入样本 X1 和 X2 相似时 （例如同一个人的两张照片）时，Y = 0；当它们不同时，Y = 1。
暹罗架构最初是为签名验证而设计的 [Bromley et al., 1993]。
最近，它们与平方指数损失（等式 17）一起用于学习相似性度量，并应用于人脸识别 [Chopra 等人，2005]。它们还与平方平方损失（等式 16）一起用于流形的无监督学习 [Hadsell 等人，2006]。
在其他应用中，单个非线性函数将X 和Y 结合起来。这种架构的一个例子是Bengio 等人的可训练语言模型[Bengio et al., 2003]。
在这个模型下，输入 X 是文本中几个连续单词的序列，答案 Y 是文本中的下一个单词。由于许多不同的单词可以跟在特定的单词序列后面，因此架构必须允许 Y 的多个值具有较低的能量。作者使用多层神经网络作为函数 G(W, X, Y )，并选择使用负对数似然损失来训练它。由于 Y 的基数很高（等于英语词典的大小），他们不得不使用近似值 （重要性采样）并且必须在集群机器上训练系统。
当前部分经常提到能量在 W 中为线性或二次方，损失函数在 W 中为凸的架构，但重要的是要记住，大部分讨论同样适用于更复杂的架构，正如我们稍后会看到的。
潜在变量架构
能量最小化是一种表示一般推理过程的便捷方法。在通常情况下，给定观测变量 X，最小化要预测的变量 Y 的能量。在训练期间，会为每个训练样本提供正确的 Y 值。然而，在许多应用中，使用依赖于一组隐藏变量 Z 的能量函数很方便，即使在训练期间，我们也从未（或很少）知道这些隐藏变量的正确值。例如，我们可以想象训练@fig-02(b) 中所示的人脸检测系统 使用无法获得面部比例和姿势信息的数据。对于这些架构，给定变量 X 和 Y 集的推理过程涉及最小化这些未知变量 Z：
\[E(Y,X)=\min_{Z\in\mathcal{Z}}E(Z,Y,X)。 \tag{41}\]
此类隐藏变量称为“潜在变量”，与概率建模中的概念类似。\(E(Y, X)\) 的求值涉及 Z 的最小化，这一事实对迄今为止描述的方法没有显著影响，但潜在变量的使用如此普遍，因此值得特别处理。
具体来说，通过将存在潜在变量时的推理过程视为对 Y 和 Z 的同时最小化，可以获得一些见解：
\[Y^*=\mathrm{argmin}_{Y\in\mathcal{Y},Z\in\mathcal{Z}}E(Z,Y,X). \tag{42}\]
潜在变量可以看作是寻找最佳输出 Y 的中间结果。此时，有人可能会认为 Z 和 Y 变量之间没有概念上的区别：Z 可以简单地折叠到 Y 中。区别出现在训练过程中：我们获得了许多训练样本的正确 Y 值，但我们从未获得正确的 \(Z\) 值。
在建模过程的隐藏特征可以从观察中推断出来但无法直接预测的情况下，潜在变量非常有用。识别问题就是这样一个例子。例如，在人脸识别中，人的性别或面部方向可能是一个潜在变量。了解这些值将使识别任务变得容易得多。同样，在不变对象识别中，对象的姿势参数（位置、方向、尺度）或照明可能都是潜在变量。它们在必须同时执行顺序数据分割和识别任务的问题中起着至关重要的作用。一个很好的例子是语音识别，其中句子分割成单词和单词分割成音素必须与识别同时进行，但在训练期间很少能正确分割成音素。同样，在手写识别中，单词分割成字符应该与识别同时进行。本节讨论了潜在变量在人脸识别中的使用，第 7.3 节描述了手写识别的潜在变量架构。
潜在变量架构的一个例子
为了说明潜在变量的概念，我们考虑人脸检测任务，首先要解决一个简单的问题，即确定小图像中是否存在人脸。假设我们有一个人脸检测函数 Gface(X) 它以一个小图像窗口作为输入并产生标量输出。当人脸填满输入图像时，它会输出一个小值，如果没有人脸（或者只有一部分人脸或一张小脸），它会输出一个大值。Figure 8(a) 显示了围绕此函数构建的基于能量的人脸检测器。变量 Y 控制二进制开关的位置（1 =“人脸”，0 =“非人脸”）。当 Y = 1 时，输出能量等于 Gface(X)，当 Y = 0 时，等于固定阈值 T：
\[E(Y,X)=Y G_{\mathrm{face}}(X)+(1-Y)T.\]
如果 Gface(X) < T 且 0 ，则最小化该能量函数的 Y 值为 1（面） （非面孔）否则。
现在让我们考虑更复杂的任务，即在一张大图像中检测和定位一张脸。我们可以将 Gface(X) 函数应用于大图像中的多个窗口，计算哪个窗口产生最低的 Gface(X) 值，并检测
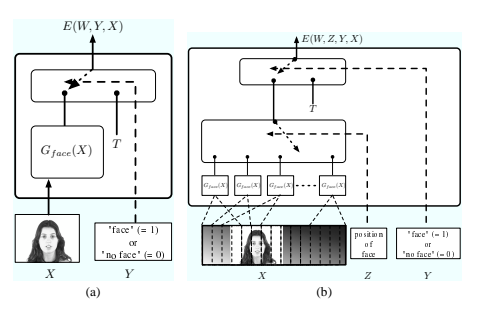
如果值低于 T ，则在该位置处进行 face 转换。此过程由 Figure 8(b) 中所示的基于能量的架构实现。潜在“位置”变量 Z 选择将 G_face 函数的 K 个副本中的哪一个路由到输出能量。能量函数可以写成
\[E(Z,Y,X)=Y\left[\sum_{k=1}^{K}\delta(Z-k)G_{\rm face}(X_{k})\right]+(1-Y)T, \tag{43}\]
其中 Xk 是图像窗口。定位图像中得分最高的位置在于最小化 Y 和 Z 的能量。结果 Y 的值将指示是否找到了脸部，结果 Z 的值将指示位置。
概率隐变量
当给定 X 和 Y 的潜在变量的最佳值不明确时，可以考虑通过边缘化潜在变量来组合各种可能值的贡献，而不是针对这些变量进行最小化。
当存在潜在变量时，吉布斯分布给出的 Y 和 Z 的联合条件分布为：
\[P(Z,Y|X)=\frac{e^{-\beta E(Z,Y,X)}}{\int_{y\in Y,z\in Z}e^{-\beta E(y,z,X)}}. \tag{44}\]
对 Z 进行边际化可得出：
\[P(Y|X)=\frac{\int_{z\in Z}e^{-\beta E(Z,Y,X)}}{\int_{y\in Y,z\in Z}e^{-\beta E(y,z,X)}}. \tag{45}\]
在对 Z 进行边缘化后，找到最佳 Y 可简化为：
\[Y^{*}=\operatorname{argmin}_{Y\in{\mathcal{Y}}}-{\frac{1}{\beta}}\log\int_{z\in{\mathcal{ Z}}}e^{-\beta E(z,Y,X)}. \tag{46}\]
这其实是一种传统的基于能量的推理，只是将能量函数从\(E(Z,Y,X)\)重新定义为\({\mathcal{F}}({\mathcal{Z}})=-{\frac{1}{\beta}}\log\int_{z\in{\mathcal{Z}}}e^{-\beta E(z,Y,X)}\)，即集合\(\{E(z,Y,X),z\in\mathcal{Z}\}\)的自由能。当\(\beta\to\infty\)（零温度）时，上述通过边缘化得到的推理公式简化为通过最小化得到的先前推理公式。
基于能量的模型的损失函数分析
本节讨论了损失函数必须满足的条件，以便最小化损失函数后得到的模型能够得出正确的答案。为了直观地了解这个问题，我们首先描述了一些简单的实验，其中使用某些架构和损失函数的组合来学习一个简单的数据集，结果各不相同。第 5.2 节将介绍更正式的处理方法。
“好”和“坏”的损失函数
考虑学习计算数字平方的函数的问题： Y = f(X)，其中 f(X) = X2。虽然这对于学习机器来说只是个小问题，但它对于演示能量函数和损失函数协同工作的设计中涉及的问题很有用。对于以下实验，我们使用 200 个样本 (Xi, Y i) 的训练集，其中 Y i = Xi 2，在 −1 和 +1 之间随机采样，均匀分布。
首先，我们使用@fig-09(a) 中所示的架构。输入 X 通过参数函数 GW 传递，该函数产生标量输出。使用差值的绝对值（L1 范数）将输出与所需答案进行比较：
\[E(W,Y,X)=||G_W(X)-Y||_1. \tag{47}\]
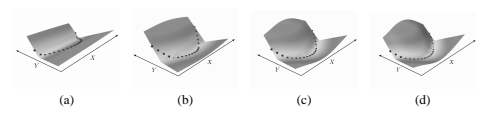
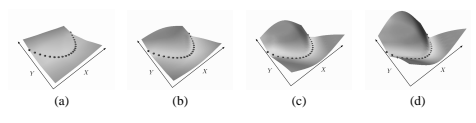
任何合理的参数化函数系列都可用于 GW 。对于这些实验，我们选择了一个两层神经网络，其中有 1 个输入单元、20 个隐藏单元（带有 S 型函数）和 1 个输出单元。Figure 10(a) 显示了变量 X 和 Y 空间中能量函数的初始形状，使用一组随机初始参数 W。深色球体标记了一些训练样本的位置。
首先，使用能量损失（Equation 5）训练简单的架构：
\[{\cal L}_{\rm 能量}(W,{\cal S})=\frac{1}{P}\sum_{i=1}^{P}E(W,Y^{i},X^{i})=\frac{1}{P}\sum_{i=1}^{P}||G_{W}(X)-Y||_{1}. \tag{48}\]
这对应于经典形式的稳健回归。学习过程可以看作是在训练样本（Figure 10 中的球体）的位置处拉下能量表面，而不考虑能量表面上的其余点。
对于任何 X，作为 Y 函数的能量表面都具有具有固定斜率的 V 形。
通过改变函数 GW (X)，该 V 的顶点可以针对不同的 Xi 移动。通过将 V 的顶点置于 Y = X2 的位置（对于任何 X 值），可以将损失最小化，这会使所有其他答案的能量变大，因为 V 具有一个最小值。Figure 10 显示了在使用简单随机梯度下降进行训练期间固定间隔的能量表面形状。在训练集进行几次迭代后，能量表面会呈现正确的形状。使用更复杂的损失函数（例如 NLL 损失或感知器损失）将产生与能量损失完全相同的结果，因为在这种简单的架构下，它们的对比项是恒定的。
考虑一个稍微复杂一点的架构，如@fig-09(b) 所示，用于学习相同的数据集。在这个架构中，X 通过函数 G1W1，Y 通过函数 G_2W2。在实验中，两个函数都是两层神经网络，有 1 个输入单元、10 个隐藏单元和 10 个输出单元。能量是它们的 10 维输出之间的差异的 L_1 范数：
\[E(W,X,Y)=||G_{1_{W_1}}(X)-G_{2_{W_2}}(Y)||_1, \tag{49}\]
其中 W = [W1W2]。使用能量损失训练此架构会导致能量表面崩溃。Figure 11 显示了训练过程中能量表面的形状；能量表面基本变为平坦。发生了什么？对于给定的 X，作为 Y 函数的能量形状不再固定。由于能量损失，没有机制可以防止 G1 和 G2 忽略其输入并产生相同的输出值。这会导致崩溃的解决方案：能量表面是平坦的，并且在任何地方都等于零。
现在考虑相同的架构，但使用 square-square 损失进行训练：
\[L(W,Y^{i},X^{i})=E(W,Y^{i},X^{i})^{2}-\left(max(0,m-E(W,\bar{Y}^{i},X^{i}))\right)^{2}. \tag{50}\]
这里 m 是正边距，Y¯ 是最令人反感的错误答案。损失中的第二项明确地通过推高能量可能低于所需答案的点来防止能量崩溃。Figure 12 显示了训练过程中能量函数的形状；表面成功达到了所需的形状。
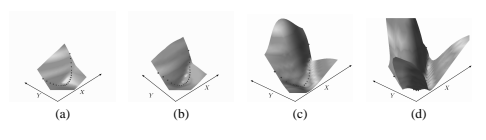
与该架构配合良好的另一个损失函数是负对数似然损失：
\[L(W,Y^{i},X^{i})=E(W,Y^{i},X^{i})+\frac{1}{\beta}\log\left(\int_{y\in\mathcal{Y}}e^{-\beta E(W,y,X^{i})}\right). \tag{51}\]
第一项下拉所需答案的能量，而第二项上推所有答案的能量，特别是那些能量最低的答案。请注意，与所需答案相对应的能量也出现在第二项中。使用负对数似然损失在不同间隔下的能量函数形状如图 13 所示。学习速度比平方-平方损失快得多。最小值更深，因为与平方-平方损失不同，错误答案的能量被推到无穷大（尽管力度在减小）。然而，负对数似然损失的每次迭代都涉及更多的工作，因为当第二项导数不存在解析表达式时，上推每个错误答案的计算成本很高。在这个实验中，使用了一种简单的采样方法：积分近似于 Y 方向上 20 个点的总和，这些点在 -1 和 +1 之间有规律地分布。因此，每次学习迭代都需要计算 20 个位置的能量梯度，而平方-平方损失的情况则需要计算 2 个位置的能量梯度。但是，对于平方损失，必须考虑找到最令人讨厌的错误答案的成本。
NLL 损失的一个重要方面是它不受能量值的全局偏移影响，并且仅取决于给定 X 的 Y 能量之间的差异。因此，所需答案对于不同的 X 可能具有不同的能量，并且可能不为零。这有一个重要的后果：如果不考虑所有其他答案的能量，答案的质量就不能通过该答案的能量来衡量。
在本节中，我们看到了训练四种架构和损失函数组合的结果。在第一种情况下，我们使用了一个简单的架构和一个简单的能量损失，这是令人满意的。系统架构中的约束会自动导致不需要的答案的能量增加，同时减少所需答案的能量。在第二种情况下，使用了更复杂的架构和简单的能量损失，机器因损失中缺少对比项而崩溃。在第三种和第四种情况下，使用了与第二种情况相同的架构，但损失函数包含明确的对比项。在这些情况下，机器的表现符合预期，没有崩溃。
良好损失函数的充分条件
在上一节中，我们借助说明性实验给出了一些关于哪些损失函数好哪些损失函数不好的直觉。本节将对这一主题进行更正式的处理。首先，陈述一组充分条件。
能量函数和损失函数必须满足这些条件才能保证在基于能量的环境中工作。然后我们从这些条件的角度讨论了前面介绍的损失函数的质量。
能量条件
一般在基于能量的学习中，推理方法选择能量最小的答案，因此对一个样本(Xi,Yi)进行正确推理的条件如下。
条件 1 对于样本 (Xi, Y i)*，如果
\[E(W,Y^{i},X^{i})<E(X,Y,X^{i}),\,\forall Y\in{\cal Y}\,\,\mbox{and}\,\,Y\neq Y^{i}. \tag{52}\]
换句话说，如果期望答案 Y 的能量 iis 小于所有其他答案 Y 的能量。
为了确保正确答案具有稳健稳定性，我们可以选择将其能量设置为比错误答案的能量低正差 m。如果 Y¯ i 表示最令人反感的错误答案，则答案正确差 m 的条件如下。
条件 2 对于变量 Y 和样本 (Xi, Y i) 和正边际 m，如果推理算法将给出正确答案 Xiif
\[E(W,Y^i,X^i)<E(W,\bar{Y}^i,X^i)-m. \tag{53}\]
损失函数的充分条件
如果系统要产生正确的答案，则损失函数的设计应使得最小化损失函数会导致 E(W, Y i, Xi) 低于 E(W, Y¯ i, Xi) m 左右。由于只有这两个能量的相对值才重要，我们只需要考虑这两个能量在二维空间中的损失函数切片的形状。例如，在 Y 是从 1 到 k 的整数集的情况下，损失函数可以写成：
\[L(W,Y^{i},X^{i})=L(Y^{i},E(W,1,X^{i}),\ldots,E(W,k,X^{i}))。 \tag{54}\]
该损失在 E(W, Y i, Xi) 和 E(W, Y¯ i, Xi) 空间中的投影可看作是由其他 k − 2 个能量参数化的函数 Q：
\[L(W,Y^i,X^i)=Q_{[E_y]}(E(W,Y^i,X^i),E(W,\bar{Y}^i,X^i)), \tag{55}\]
其中参数 \([E_{y}]\) 包含除 \(Y^i\) 和 \(\bar{Y}^{i}\) 之外的所有 Y 值的能量向量。
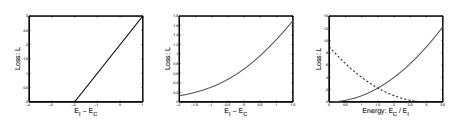
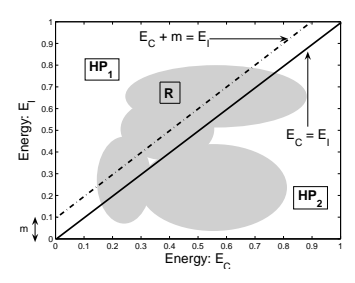
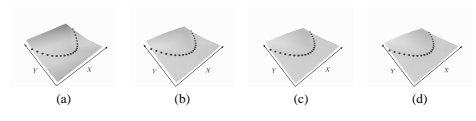
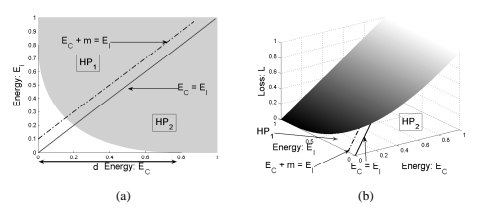
我们假设存在至少一组参数 W，对于单个训练样本 (Xi, Y i)，条件 2 得到满足。显然，如果不存在这样的 W，就不可能存在任何损失函数，其最小化会导致条件 2。为了符号简单起见，让我们用 EC（如“正确能量”）和 E(W, Y¯ i, Xi) 表示与训练样本 (Xi, Y i) 相关的能量 E(W, Y i, Xi) 由 EI（如“不正确的能量”）。考虑由 EC 和 EI 形成的平面。为了说明起见，Figure 17(a) 显示了 square-square 损失函数的三维图，其中横坐标是 EC ，纵坐标是 EI 。第三轴给出了 EC 和 EI 对应值的损失值。一般来说，损失函数是这个 3D 空间中的一组 2D 曲面，其中每个曲面对应于除 EC 和 EI 之外的所有能量的一个特定配置。图中的实线红线对应于 2D 平面中 EC = EI 的点。虚线蓝线对应于边缘线 EC +m = EI 。让两个半平面 EC +m < EI 且 EC + m ≥ EI 分别记为 HP1 和 HP2。
假设 R 为可行区域，定义为 W ∈ W 的所有可能值对应的值集 (EC , EI )。该区域可以是非凸的、不连续的、开放的或一维的，并且可以位于平面上的任何位置。它在 中以阴影显示
图? 14. 由于我们假设存在一个满足条件 2 的解，因此 R 必须与半平面 HP1 相交。
假设两个点 \((e_1,e_2)\) 和 \((e_1^{\prime},e_2^{\prime})\) 属于可行域 R，使得 \((e_1,e_2)\in{HP_1}\)（即 \(e_1+m<e_2\)）和 \((e_1^{\prime},e_2^{\prime})\in HP_2\)（即 \(e_1^{\prime}+m\geq e_2^{\prime}\)）。现在我们准备给出损失函数的充分条件。
条件 3 设 \((X^i,Y^i)\) 为第 i 个训练样本，m 为正边际。如果存在至少一个点 (e1, e2)，且 \(e_1+m<e_2\)，使得对于所有点 \((e_{1}^{\prime},e_{2}^{\prime})\)，且 \(e_1^{\prime}+m\geq e_2^{\prime}\)，则最小化损失函数 L 将满足条件 1 或 2
\[Q_{[E_{y}]}(e_{1},e_{2})<Q_{[E_{y}]}(e^{\prime}_{1},e^{\prime}_{2}), \tag{56}\]
\[L(W,Y^{i},X^{i})=Q_{[E_{y}]}(E(W,Y^{i},X^{i}),E(W,\bar{Y}^{i},X^{i})). \tag{57}\]
换句话说，EC 和 EI 空间中的损失函数曲面应该使得可行域 R 与半平面 HP1 相交的部分中至少存在一个点，使得该点处的损失函数值小于 R 与半平面 \(HP_2\) 相交的部分中所有其他点处的损失函数值。
请注意，这只是充分条件，而不是必要条件。可能存在不满足此条件但其最小化仍满足条件 2 的损失函数。
| 损失（公式 #） | 公式 | 利润 | |
|---|---|---|---|
| 能量损失（6） | E（W，Y i，Xi） | 无 | |
| 感知器 (7) | E(W, Y i , Xi ) − minY ∈Y E(W, Y, Xi ) | E(W, Y i , Xi ) − minY ∈Y 0 | |
| 铰链 (11) | 最大 0，m + E(W，Y i，Xi) − E(W，Y¯ i，Xi) | m | |
| log (12) | log 1 + e E(W,Y i ,Xi )−E(W,Y¯ i ,Xi ) | > 0 | |
| LVQ2 (13) | 最小 M，最大(0，E(W，Y i ，Xi) − E(W，Y¯ i ，Xi) | 0 | |
| −(E(W,Y i ,Xi )−E(W,Y¯ i ,Xi )) −1 | > 0 | ||
| MCE (15) | 1 + e | 2 − max(0, m − E(W, Y¯ i , Xi ))2 | m |
| 平方-平方 (16) | E(W, Y i , Xi ) | ||
| 平方指数 (17) | E(W, Y i , Xi ) 2 + βe−E(W,Y¯ i ,Xi ) | > 0 | |
| NLL/MMI (23) | E(W, Y i , Xi ) + 1 β log R y∈Y e −βE(W,y,Xi ) | > 0 | |
| −βE(W,Y i ,Xi )/R y∈Y e −βE(W,y,Xi ) | > 0 | ||
| 中东 (27) | 1 − e |
哪些损失函数是好的或坏的
Table 1 列出了几个损失函数，以及它们满足条件 3 的边距值。能量损失标记为“无”，因为它不满足一般架构的条件 3。感知器损失和 LVQ2 损失以零边距满足条件 3。所有其他函数都以严格的正边距值满足条件 3。
能量损失
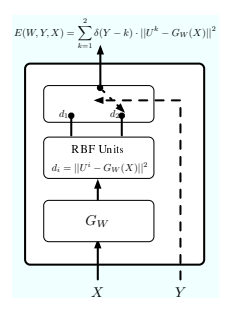
能量损失通常是一种不好的损失函数，但对于某些形式的能量来说，它是一种很好的损失函数。例如，考虑以下形式的能量函数
\[E(W,Y^{i},X^{i})=\sum_{k=1}^{K}\delta(Y^{i}-k)||U^{k}-G_{W}(X^{i})||^{2}. \tag{58}\]
该能量将函数 GW 的输出通过 K 个径向基函数 （每个类别对应一个）其中心是向量 U k. 如果中心 U k 是固定的且不同的，那么能量损失满足条件 3，因此是一个好的损失函数。
为了理解这一点，我们来考虑二分类的情况（K > 2 的推理也是同样的道理）。系统架构如图 15 所示。
令 \(d=||U^{1}-U^{2}||^{2}\)、\(d_1=||U^1-G_W(X^i)||^2\) 和 \(d_{2}=||U^{2}-G_{W}(X^{i})||^{2}\)。由于 U^1 和 U^2 是固定且不同的，因此对于所有 GW ，d1 + d2 都有一个严格正的下限。由于只是一个二分类问题，EC 和 EI 直接对应于这两个类的能量。在 (EC , EI ) 平面中，损失函数的任何部分都不存在 EC + EI ≤ d。定义损失函数的区域在图 16(a) 中用阴影表示。损失函数的确切形状如图 16(b) 所示。从图中可以看出，只要 d ≥ m，损失函数就满足条件 3。我们得出结论，这是一个很好的损失函数。
然而，当 RBF 中心 U^1 和 U^2 不固定且允许学习时，就不能保证 \(d_1+d_2 \geq d\)。然后 RBF 中心可能会变得相等，并且所有输入的能量可能会变为零，从而导致能量表面塌陷。通过在损失函数中加入对比项可以避免这种情况。
广义感知器损失
广义感知器损失的边际为零。因此，它可能导致能量表面塌陷，通常不适合训练基于能量的模型。
然而，没有边际并不总是致命的 [LeCun et al., 1998a, Collins, 2002]。首先，崩溃解决方案集只是参数空间的一小部分。其次，虽然没有什么能阻止系统达到崩溃解决方案，但也没有什么能驱使系统走向崩溃解决方案。因此，达到崩溃解决方案的概率非常小。
广义保证金损失
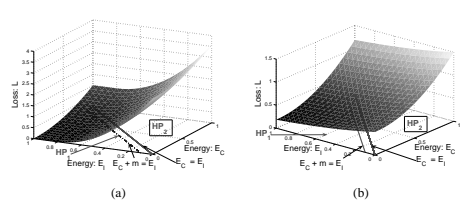
现在我们考虑 平方-平方 和 平方-指数 损失。对于二分类情况，EC 和 EI 空间中损失的表面形状如图 17 所示。可以清楚地看到，HP1 中至少存在一个点 (e1, e2)，使得
\[Q_{[E_y]}(e_1,e_2)<Q_{[E_y]}(e_1',e_2'), \tag{59}\]
对于 \(HP_2\) 中的所有点 \((e_1',e_2')\)。这些损失函数满足条件 3。
负对数似然损失
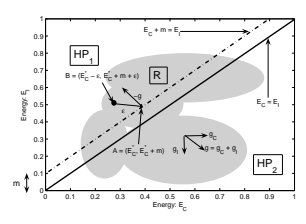
负对数似然损失满足条件 3 并不明显。证明如下。
对于任何固定参数 W 和一个样本 (Xi, Y i)，考虑损失相对于正确答案 \(Y^i\) 的能量 EC 和最令人反感的错误答案 \(\bar{Y}_{i}\) 的能量 EI 的梯度。我们有
\[g_{C}=\frac{\partial L(W,Y^{i},X^{i})}{\partial E_{C}}=1-\frac{e^{-E(W,Y^{i},X^{i})}}{\sum_{Y\in\mathcal{Y}}e^{-E(W,Y,X^{i})}}, \tag{60}\]
和
\[g_{I}={\frac{\partial L(W,Y^{i},X^{i})}{\partial E_{I}}}=-{\frac{e^{-E(W,\bar{Y}^{i},X^{i})}}{\sum_{Y\in{\mathcal{Y}}}e^{-E(W,\bar{Y},X^{i})}}}. \tag{61}\]
显然，对于任何能量值，gC > 0 且 gI < 0。EC 和 EI 空间中任何一点的梯度总体方向如图 18 所示。可以得出结论，从 HP2 到 HP1 时，损失单调递减。
现在我们需要证明 HP1 中至少存在一个点，该点的损失小于 HP2 中的所有点。假设 A = (E∗C , E∗C + m) 是边际上的一个点
损失最小的线。E∗C 是此点的正确能量值。也就是说，
\[E_{C}^{*}=\operatorname{argmin}\{Q_{[E_{y}]}(E_{C},E_{C}+m)\}. \tag{62}\]
因为从上面的讨论来看，损失函数 Q[Ey] 的梯度的负值始终 点（尤其是边缘线上的点）位于 HP1 内部的方向， 损失的单调性，我们可以得出
\[Q_{[E_{y}]}(E_{C}^{*},E_{C}^{*}+m)\leq Q_{[E_{y}]}(E_{C},E_{I}), \tag{63}\]
其中 \(E_C+m>E_I\)。
考虑一个点 \(B\)，它距离点 \((E_C^*,E_C^*+m)\) 的距离为 \(\epsilon\)，并且位于 HP_1 内（参见@fig-18）。这就是点
\[(E_{C}^{*}-\epsilon,E_{C}^{*}+m+\epsilon). \tag{64}\]
对此点的损失值进行一阶泰勒展开，我们得到
\[Q_{[E_{y}]}(E_{C}^{*}-\epsilon,E_{C}^{*}+m+\epsilon)\] \[=Q_{[E_{y}]}(E_{C}^{*},E_{C}^{*}+m)-\epsilon\frac{\partial Q_{[E_{y}]}}{\partial E_{C}}+\epsilon\frac{\partial Q_{[E_{y}]}}{\partial E_{I}}+O(\epsilon^{2})\] \[=Q_{[E_{y}]}(E_{C}^{*},E_{C}^{*}+m)+\epsilon\left[\frac{\partial Q_{[E_{y}]}}{\partial E_{C}}+\frac{\partial Q_{[E_{y}]}}{\partial E_{I}}\right]\left[\begin{array}{c}-1\\ 1\end{array}\right]+O(\epsilon^{2})。 \tag{65}\]
从前面的讨论可以看出，右边的第二项是负数。因此，对于足够小的ε，我们有
\[Q_{[E_{y}]}(E_{C}^{*}-\epsilon,E_{C}^{*}+m+\epsilon)<Q_{[E_{y}]}(E_{ C}^{*},E_{C}^{*}+m). \tag{66}\]
因此，我们得出结论，HP1 中至少存在一个点，其损失小于 HP2 中所有点的损失。
请注意，最令人反感的错误答案 EI 的能量受次之最令人反感的错误答案的能量值限制。因此，我们只需考虑 EI 的有限范围，而点 B 不能位于无穷远处。
高效推理：非概率因子图
本节讨论基于能量的高效推理这一重要问题。序列标记问题和其他具有结构化输出的学习问题通常可以使用能量函数进行建模，其结构可用于高效的推理算法。
使用 EBM 进行学习和推理涉及最小化答案集 \(\mathcal{Y}\) 和潜在变量 \(\mathcal{Z}\) 的能量。当 \(\mathcal{Y}\times\mathcal{Z}\) 的基数很大时，这种最小化可能变得难以解决。解决该问题的一种方法是利用能量函数的结构来有效地执行最小化。一种可以利用该结构的情况是，当能量可以表示为各个函数（称为因子）的总和时，每个函数都依赖于 Y 和 Z 中变量的不同子集。这些依赖关系最好以因子图的形式表示 [Kschischang et al., 2001, MacKay, 2003]。因子图是图形模型或信念网络的一般形式。
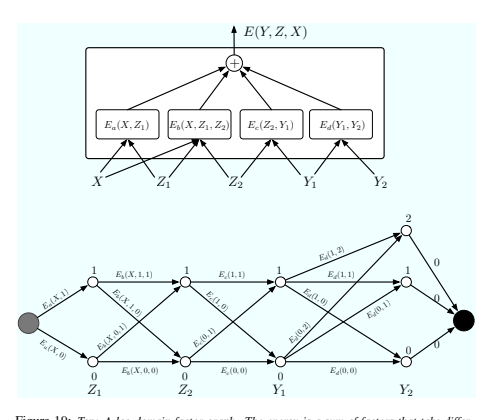
图形模型通常用于通过直接编码变量之间的依赖关系来表示变量的概率分布。乍一看，很难将图形模型与概率建模区分开来（见其原名：“贝叶斯网络”）。然而，因子图可以在概率建模的背景之外进行研究，EBM 学习适用于它们。
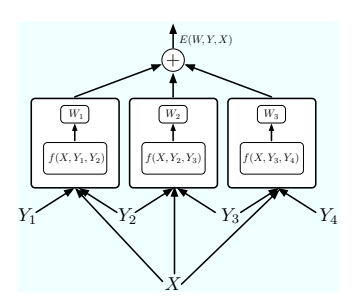
图? 19（顶部）显示了因子图的一个简单示例。能量函数是四个因子的总和：
\[E(Y,Z,X)=E_a(X,Z_1)+E_b(X,Z_1,Z_2)+E_c(Z_2,Y_1)+E_d(Y_1,Y_2), \tag{67}\]
其中 \(Y=[Y_1,Y_2]\) 是输出变量，\(Z=[Z_1,Z_2]\) 是潜在变量。
每个因素都可以看作是其输入变量值之间的软约束。推理问题在于找到：
\[(\bar{Y},\bar{Z})=\mathrm{argmin}_{y\in\mathcal{Y},z\in\mathcal{Z}}\left(E_{a}(X,z_{1})+E_{b}(X,z_{1},z_{2})+E_{c}(z_{2},y_{1})+E_{d}(y_{1},y_{2})\right). \tag{68}\]
该因子图代表一个结构化输出问题，因为因子 Ed 对 Y 1 和 Y 2 之间的依赖关系进行编码（可能通过禁止某些值的组合）。
假设 Z1、Z2 和 Y1 是离散二进制变量，Y2 是三元变量。X 域的基数无关紧要，因为 X 始终是可观察的。给定 X，Z 和 Y 的可能配置数为 2 × 2 × 2 × 3 = 24。
通过穷举搜索的简单最小化算法将对整个能量函数进行 24 次评估（96 次单因子评估）。但是，我们注意到，对于给定的 X，Ea 只有两种可能的输入配置：Z1 = 0 和 Z1 = 1。同样，Eb 和 Ec 只有 4 种可能的输入配置，而 Ed 有 6 种。因此，不需要超过 2 + 4 + 4 + 6 = 16 次单因子评估。可能配置的集合可以用图（网格）表示，如@fig-19（底部）所示。每列中的节点代表单个变量的可能值。每个边都由因子的输出能量加权，以对应其输入变量的值。通过这种表示，从起始节点到终止节点的一条路径代表所有变量的一种可能配置。沿路径的权重之和等于相应配置的总能量。因此，推理问题可以简化为在此图中搜索最短路径。这可以使用动态规划方法（例如 Viterbi 算法或 A* 算法）来实现。成本与边数 (16) 成正比，而边数通常比路径数小得多。要计算 E(Y, X) = minz∈Z E(Y, z, X)，我们遵循相同的程序，但我们将图限制为与 Y 的规定值兼容的弧子集。
上述过程有时称为最小和算法，它是图模型中传统最大乘积的对数域版本。该过程可以很容易地推广到因子图，其中因子以两个以上的变量作为输入，以及具有树结构而不是链结构的因子图。但是，它仅适用于二分树（无循环）的因子图。当图中存在循环时，最小和算法在迭代时可能会给出近似解，或者根本不会收敛。在这种情况下，可以使用下降算法，例如模拟退火。
如第 4 节所述，可以通过最小化或边缘化来处理变量。计算与计算负对数似然损失的对比项（对数分区函数）所需的计算相同， 因此我们不做区分。负对数似然损失函数中的对比项是：
\[-\frac{1}{\beta}\log\int_{Y\in{\mathcal{Y}},\ z\in{\mathcal{Z}}}e^{-\beta E(Z,Y,X)}, \tag{69}\]
或者简单地
\[-\frac{1}{\beta}\log\int_{Y\in\mathcal{Y}}e^{-\beta E(Y,X)}, \tag{70}\]
当不存在潜在变量时。
乍一看，这似乎很难解决，但计算可以像最小和算法一样分解。结果就是所谓的对数域中的前向算法。值向前传播，从左侧的起始节点开始，并沿着网格中的箭头传播。每个节点 k 计算一个量 αk：
\[\alpha_{k}=-\frac{1}{\beta}\log\sum_{j}e^{-\beta(E_{k j}+\alpha_{j})}, \tag{71}\]
其中 Ejk 是与节点 j 和节点 k 之间的边相连的能量。最终节点的 α 是方程 70 中的数量。对于较大的 β 值，该过程简化为最小和算法。
在更复杂的因子图中，因子以两个以上变量作为输入，或具有树结构，此过程推广为对数域中的非概率形式的信念传播。对于循环图，该过程可以迭代，并且如果它完全收敛，则可能导致方程 70 的近似值 [Yedidia 等人，2005 年]。
上述程序是构建具有结构和/或顺序输出的模型的重要组成部分。
Ebms 与内部标准化模型
值得注意的是，在上述讨论中，我们从未需要操纵正则化概率分布。唯一需要操纵的量是能量。这与隐马尔可夫模型和传统贝叶斯网络形成对比。在 HMM 中，节点的传出转移概率必须总和为 1，并且发射概率必须正确正则化。这确保了序列上的整体分布是正则化的。同样，在有向贝叶斯网络中，条件概率表的行也是正则化的。
EBM 操纵能量，因此无需进行归一化。当能量转换为概率时，对 Y 的归一化是该过程的最后一步。这种“后期归一化”的想法解决了与 HMM 和贝叶斯网络的内部归一化相关的几个问题。第一个问题是所谓的“标签偏差问题”，由 Bottou [Bottou, 1991] 首次指出：离开给定状态的转换相互竞争，但不与模型中的其他转换竞争。因此，状态中传出转换较少的路径往往比状态中传出转换较多的路径具有更高的概率。这似乎是人为的限制。为了规避这个问题，Denker 和 Burges 在手写和语音识别的背景下首次提出了一种后期归一化方案 [Denker and Burges, 1995]。标签偏差问题的另一种形式是 LeCun 等人在 [LeCun et al., 1998a] 中讨论的“缺失概率质量问题”。他们还利用后期规范化方案来解决这个问题。规范化模型将概率质量分布在系统明确建模的所有答案中。为了应对“垃圾”或其他不可预见和未建模的输入，设计人员通常必须添加所谓的背景模型，从明确建模的答案集合中拿走一些概率质量。这可以被理解为一种隐晦的消除规范化约束的方法。换句话说，由于每个显式规范化都是错误处理不可预见事件的另一个机会，因此应该努力将模型中的显式规范化数量降至最低。最近通过消除规范化成功处理标签偏差问题的一个示例是 McCallum、Freitag 和 Pereira 的最大熵马尔可夫模型 [McCallum et al., 2000] 与 Lafferty、McCallum 和 Pereira 的条件随机场 [Lafferty et al., 2001] 之间的比较。
第二个问题是控制不同性质的概率分布的相对重要性。在 HMM 中，发射概率通常是高维空间（通常为 10 到 100）中的高斯混合，而转移概率是几个转移上的离散概率。前者的动态范围比后者大得多。因此，转移概率在整体可能性中几乎不计入任何因素。从业者通常会将转移概率提高到某个幂以增加其影响力。这种技巧在概率框架中很难证明其合理性，因为它破坏了规范化。在基于能量的框架中，没有必要为违反规则找借口。任意系数可以应用于模型中的任何能量子集。规范化总是可以在最后执行。
第三个问题涉及判别学习。判别训练通常使用基于梯度的迭代方法来优化损失。在每次通过梯度方法更新参数后执行归一化步骤通常很复杂、昂贵且效率低下。EBM 方法消除了这个问题 [LeCun et al., 1998a]。更重要的是，内部归一化 HMM 和贝叶斯网络的原因与判别训练它们的想法有些矛盾。归一化仅对生成模型是必要的。
Ebms 用于序列标记和结构化输出
对符号序列或向量序列进行分类或标记的问题长期以来一直是多个技术社区关注的话题。最早和最显著的例子是语音识别。20 世纪 80 年代末，人们提出了判别学习方法来训练基于 HMM 的语音识别系统 [Bahl 等人，1986 年，Ljolje 等人，1990 年]。这些 HMM 方法大大提高了语音识别系统的准确性，至今仍是一个活跃的研究课题。
随着多层神经网络训练程序的出现，一些研究小组提出了将神经网络和时间对齐方法结合起来进行语音识别。时间对齐可以通过一组参考词的弹性模板匹配（动态时间扭曲）或使用隐马尔可夫模型来实现。主要挑战之一是设计一种集成训练方法，用于同时训练神经网络和时间对齐模块。在 20 世纪 90 年代初期，一些作者提出了将神经网络与动态时间规整相结合的方法 [Driancourt et al., 1991a, Driancourt et al., 1991b, Driancourt and Gallinari, 1992b, Driancourt and Gallinari, 1992a, Driancourt, 1994]，以及将神经网络与 HMM 相结合的方法 [Bengio et al., 1990, Bourlard and Morgan, 1990, Bottou, 1991, Haffner et al., 1991, Haffner and Waibel, 1991, Bengio et al., 1992, Haffner and Waibel, 1992, Haffner, 1993, Driancourt, 1994, Morgan and Bourlard, 1995, Konig et al.等人，1996 年]。有关该主题的大量参考文献可在 [McDermott，1997 年，Bengio，1996 年] 中找到。大多数方法使用一维卷积网络（“时间延迟神经网络”）来增强对音高、音色和语速变化的鲁棒性。早期模型将判别分类器与时间对齐相结合，但没有集成序列级训练 [Sakoe 等人，1988 年，McDermott 和 Katagiri，1992 年，Franzini 等人，1990 年]。将类似的想法应用于手写识别更具挑战性，因为信号的二维性质使分割问题变得更加复杂。这项任务需要集成图像分割启发式方法来生成分割假设。为了对具有几何失真鲁棒性的片段进行分类，使用了 2D 卷积网络 [Bengio 等人，1993 年，LeCun 和 Bengio，1994 年，Bengio 等人，1995 年]。将分割和识别的集成学习与后期规范化相结合的通用公式产生了图形转换器网络架构 [LeCun 等人，1997 年，LeCun 等人，1998a 年]。
接下来的三节将详细描述基于能量的模型框架中的几种序列标记模型。
线性结构模型：Crf、Svmm 和 Mmmn
除了语音和手写识别中的判别训练传统之外，图形模型传统上被视为概率生成模型，并以此进行训练。然而，近年来，对判别训练的兴趣重新兴起
训练已经出现，主要受到自然语言处理中的序列标记问题的推动，特别是条件随机场 [Lafferty et al., 2001]、感知器模型 [Collins, 2002]、支持向量马尔可夫模型 [Altun et al., 2003] 和最大边际马尔可夫网络 [Taskar et al., 2003]。
这些模型可以在 EBM 设置中轻松描述。这些模型中的能量函数被假定为参数 W 的线性函数：
\[E(W,Y,X)=W^TF(X,Y), \tag{72}\]
其中 \(F(X, Y)\) 是依赖于 X 和 Y 的特征函数向量。答案 Y 是 l 个单独标签的序列（Y1, . . . , Yl），通常解释为时间序列。序列中各个标签之间的依赖关系由因子图捕获，例如@fig-20 中所示的因子图。每个因子都是可训练参数的线性函数。它取决于输入 X 和一对单独标签 （Ym，Yn）。一般来说，每个因素可能取决于两个以上的单独标签，但是为了简化符号，我们将讨论限制在成对因素上：
\[E(W,Y,X)=\sum_{(m,n)\in{\cal F}}W^{T}_{mn}f_{mn}(X,Y_{m},Y_{n})。 \tag{73}\]
这里 F 表示因子集（具有直接相互依赖关系的单个标签对的集合），Wmn 是因子 (m, n) 的参数向量，fmn(X, Ym, Yn) 是一个（固定）特征向量。全局参数向量 W 是所有 Wmn 的串联。有时假设所有因素都编码了输入和标签对之间相同类型的交互：该模型被称为同质场。
因素共享相同的参数向量和特征，能量可以简化为：
\[E(W,Y,X)=\sum_{(m,n)\in{\mathcal{F}}}W^{T}f(X,Y_{m},Y_{n})。 \tag{74}\]
能量的线性参数化确保了 W 上的相应概率分布属于指数族：
\[P(W|Y,X)={\frac{e^{-W^{T}F(X,Y)}}{\int_{w^{\prime}\in{\mathcal{W}}}e^{-w^{T}F(X,Y)}}}. \tag{75}\]
这个模型被称为线性结构模型。
我们现在介绍使用不同损失函数的各种版本的线性结构模型。第 7.2 节和第 7.3 节将介绍非线性和分层模型。
感知器损失
训练线性结构模型最简单的方法是使用感知器损失。LeCun 等人 [LeCun et al., 1998a] 建议将其用于序列标记（特别是手写识别）中的一般非线性能量函数，称之为判别性维特比训练。最近，柯林斯 [Collins, 2000, Collins, 2002] 提倡在 NLP 环境中将其用于线性结构模型：
\[{\mathcal{L}}_{\mathrm{感知器}}(W)={\frac{1}{P}}\sum_{i=1}^{P}E(W,Y^{i},X^{i})-E(W,Y^{*i},X^{i}), \tag{76}\]
其中 \(Y^{*i}=\mathrm{argmin}_{y\in\mathcal{Y}}E(W,y,X^{i})\) 是系统生成的答案。线性属性为损失提供了一个特别简单的表达式：
\[{\mathcal{L}}_{\mathrm{感知器}}(W)={\frac{1}{P}}\sum_{i=1}^{P}W^{T}\left(F(X^{i},Y^{i})-F(X^{i},Y^{*i})\right). \tag{77}\]
使用随机梯度下降来优化该损失可以得到一种简单的感知器学习规则：
\[W\gets W-\eta\left(F(X^{i},Y^{i})-F(X^{i},Y^{*i})\right)。 \tag{78}\]
如前所述，感知器损失的主要问题是缺少余量，尽管当能量是参数的线性函数时（如 Collins 模型中那样），这个问题并不致命。[LeCun et al., 1998a] 忽略了缺少余量，这在理论上可能导致稳定性问题。
边际损失：最大边际马尔可夫网络
基于边际的马尔可夫网络 [Altun et al., 2003, Altun and Hofmann, 2003, Taskar et al., 2003] 背后的主要思想是使用边际损失来训练@fig-20 的线性参数化因子图，其能量函数为公式 73。损失函数是带有 L2 正则器的简单铰链损失：
\[{\cal L}_{\rm hinge}(W)=\frac{1}{P}\sum_{i=1}^{P}\max(0,m+E(W,Y^{i},X^{i})-E(W,\bar{Y}^{i},X^{i}))+\gamma||W||^{2}. \tag{79}\]
由于能量与 W 呈线性关系，因此损耗变得特别简单：
\[{\cal L}_{\rm hinge}(W)=\frac{1}{P}\sum_{i=1}^{P}\max\left(0,m+W^{T}\Delta F(X^{i},Y^{i})\right)+\gamma||W||^{2}, \tag{80}\]
其中 \[\Delta F(X^{i},Y^{i})=F(X^{i},Y^{i})-F(X^{i},Y^{i})\]。可以使用多种技术优化此损失函数。最简单的方法是随机梯度下降。但是，铰链损失和线性参数化允许使用对偶公式，就像传统支持向量机的情况一样。哪种优化方法最合适的问题尚未解决。与神经网络训练一样，尚不清楚二阶方法是否比经过良好调整的随机梯度方法带来显着的速度提升。据我们所知，尚未发表有关此问题的系统实验研究。
Altun、Johnson 和 Hofman [Altun et al., 2003] 研究了该模型的几个版本，这些版本使用了其他损失函数，例如 Collins 提出的指数边际损失 [Collins, 2000]：
\[{\mathcal{L}}_{\mathrm{hinge}}(W)={\frac{1}{P}}\sum_{i=1}^{P}\exp(E(W,Y^{i},X^{i})-E(W,\bar{Y}^{i},X^{i}))+\gamma||W||^{2}. \tag{81}\]
该损失函数倾向于将能量 \(E(W,Y^i,X^i)\) 和 \(E(W,\bar{Y}^{i},X^{i})\) 推得尽可能远，这种影响仅受正则化的影响。
负对数似然损失：条件随机场
条件随机场 (CRF) [Lafferty 等，2001] 使用负对数似然损失函数来训练线性结构化模型：
\[{\mathcal{L}}_{\mathrm{null}}(W)={\frac{1}{P}}\sum_{i=1}^{P}E(W,Y^{i},X^{i})+{\frac{1}{\beta}}\log\sum_{y\in{\mathcal{Y}}}e^{-\beta E(W,y,X^{i})}. \tag{82}\]
能量的线性形式（等式 75）给出以下表达式：
\[{\mathcal{L}}_{\mathrm{null}}(W)={\frac{1}{P}}\sum_{i=1}^{P}W^{T}F(X^{i},Y^{i})+{\frac{1}{\beta}}\log\sum_{y\in{\mathcal{Y}}}e^{-\beta W^{T}F(X^{i},y)}. \tag{83}\]
根据公式 24，该损失关于 W 的导数为：
\[{\frac{\partial{\mathcal{L}}_{\mathrm{nll}}(W)}{\partial W}}={\frac{1}{P}}\sum_{i=1}^{P}F(X^{i},Y^{i})-\sum_{y\in{\mathcal{Y}}}F(X^{i},y)P(y|X^{i},W), \tag{84}\]
在哪里
\[P(y|X^{i},W)=\frac{e^{-\beta W^{T}F(X^{i},y)}}{\sum_{y^{\prime}\in\mathcal{Y}}e^{-\beta W^{T}F(X^{i},y^{\prime})}}\,. \tag{85}\]
此损失函数的问题是需要对所有可能的标签组合求和，因为此类组合的数量呈指数级增长（对于 l 个二进制标签序列，为 2 l）。但是，可以使用第 6 节中提到的一种高效推理算法。
CRF 的一个所谓优势是损失函数相对于 W 是凸的。然而，损失函数的凸性虽然在数学上令人满意，但似乎并不是一个显著的实际优势。尽管 CRF 的原始优化算法是基于迭代缩放的，但最近的研究表明，随机梯度方法可能更有效 [Vishwanathan 等人，2006 年]。
基于非线性图的 Ebms
20 世纪 90 年代语音和手写社区开发的图形模型判别学习方法允许对因子进行非线性参数化，主要是高斯和多层神经网络的混合。非线性因子允许对输入和标签之间高度复杂的依赖关系进行建模（例如将手写单词的像素映射到相应的字符标签）。一个特别重要的方面是使用对输入的无关变换不变（或鲁棒）的架构，例如语音中的时间膨胀或音调变化以及手写中的几何变化。这最好由分层的多层架构来处理，这些架构可以以集成的方式学习低级特征和高级表示。大多数作者已经使用一维卷积网络（时间延迟神经网络）进行语音和基于笔的手写识别[Bengio et al., 1990, Bottou, 1991, Haffner et al., 1991, Haffner and Waibel, 1991, Driancourt et al., 1991a, Driancourt et al., 1991b, Driancourt and Gallinari, 1992b, Driancourt and Gallinari, 1992a, Bengio et al., 1992, Haffner and Waibel, 1992, Haffner, 1993, Driancourt, 1994, Bengio, 1996]，并使用二维卷积网络进行基于图像的手写识别[Bengio et al., 1993, LeCun and Bengio, 1994, Bengio 等人，1995 年，LeCun 等人，1997 年，LeCun 等人，1998a]。
对于一些观察家来说，最近对线性结构模型的兴趣看起来有点像是回到过去，以及复杂性规模的倒退。线性参数化能量的一个明显优势是它们使感知器损失、铰链损失和 NLL 损失凸起。人们经常认为凸损失函数本质上更好，因为它们允许使用有效的优化算法，并保证收敛到全局最小值。然而，最近有几位作者认为凸损失函数并不能保证良好的性能，而且非凸损失在实践中可能比凸损失更容易优化，即使在没有理论保证的情况下也是如此 [Huang and LeCun，2006，Collobert 等人，2006]。
此外，有人认为凸损失函数可以使用复杂的二阶优化方法进行有效优化。然而，一个众所周知但经常被忽视的事实是，经过精心调整的随机梯度下降法在实践中通常比最复杂的二阶优化方法（在纸面上看起来更好）要快得多。这是因为随机梯度可以利用样本之间的冗余，通过基于单个样本更新参数来更新参数，而“批量”优化方法浪费了大量资源来计算精确的下降方向，通常会抵消理论上的速度优势[Becker and LeCun，1989，LeCun et al.，1998a，LeCun et al.，1998b，Bottou，2004，Bottou and LeCun，2004，Vishwanathan et al.，2006]。
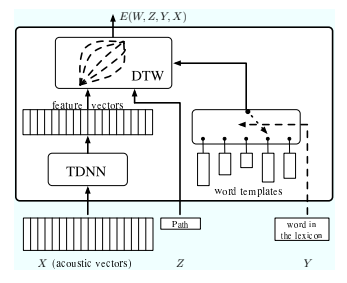
Figure 21 展示了一个语音识别系统的示例，该系统集成了时间延迟神经网络 (TDNN) 和使用动态时间规整 (DTW) 的词匹配。
首先将原始语音信号转换为声学向量序列（通常每 10 毫秒有 10 到 50 个频谱或倒谱系数）。将声学向量序列输入到 TDNN，TDNN 将其转换为高级特征序列。TDNN 中的时域子采样可用于降低特征向量的时间分辨率 [Bottou，1991]。然后将特征向量序列与单词模板进行比较。为了降低匹配对发音速度变化的敏感度，动态时间扭曲将特征序列与模板序列对齐。直观地说，DTW 在于找到将向量序列（或符号）映射到另一个序列的最佳“弹性”扭曲。可以使用动态规划（例如 Viterbi 算法或 A* 算法）有效地找到解决方案。
DTW 可以简化为在有向无环图中搜索最短路径，其中每个节点的成本是两个输入序列中两个项目之间的不匹配。因此，整个系统可以看作是一个潜在变量 EBM，其中 Y 是词典中的单词集，Z 表示每个单词的模板集和每个对齐图的路径集。最早提出的神经网络和时间对齐的集成训练是由 Driancourt 和 Bottou [Driancourt et al., 1991a] 提出的，他们提出使用 LVQ2 损失（等式 13）来训练这个系统。通过 DTW 模块反向传播梯度并进一步将梯度反向传播到 TDNN 以更新权重是一件简单的事情。
类似地，梯度可以反向传播到单词模板，以便更新它们。尽管 LVQ2 损失的边际为零，但孤立词识别仍获得了出色的结果。后来 McDermott 使用了类似的方案 [McDermott，1997]。
一种更通用的方法是结合神经网络（例如
20 世纪 90 年代，一些作者提出了一种使用隐马尔可夫模型代替 DTW 的 TDNN 算法。20 世纪 90 年代，一些作者提出了这种组合的综合训练程序。第一个提议是由 Bengio 等人提出的 [Bengio et al., 1991, Bengio et al., 1992, Bengio, 1996]，他们使用了用随机梯度下降优化的 NLL/MMI 损失，以及 Bottou [Bottou, 1991]，他提出了各种损失函数。随后，Haffner 等人在他的多状态 TDNN 中提出了类似的方法 模型 [Haffner and Waibel, 1992, Haffner, 1993]。类似的训练方法也用于手写识别。Bengio 和 LeCun 描述了一种神经网络/HMM 使用随机梯度下降优化的 NLL/MMI 损失进行全局训练的混合 [Bengio 等人，1993 年，LeCun 和 Bengio，1994 年]。此后不久，Konig 等人提出了 REMAP 方法，该方法将期望最大化算法应用于 HMM，以便为基于神经网络的声学模型产生目标输出 [Konig 等人，1996 年]。
神经网络/HMM 混合系统的基本架构与@fig-21 中的系统类似，只是单词（或语言）模型是概率有限状态机而不是序列。每个节点的发射概率通常是对神经网络产生的输出向量序列进行运算的简单高斯分布。
唯一的挑战是通过 HMM 网格反向传播梯度来计算相对于神经网络输出的损失梯度。由于该过程与图变换器网络中使用的过程非常相似，我们将在下一节中进行说明。
需要注意的是，之前很多作者提出了结合单独训练的判别分类器和语音和手写对齐方法的方法，但没有使用集成训练方法。
基于层次图的 Ebms：图变换器网络
第 7.2 和 7.1 节讨论了推理和学习涉及边缘化或最小化动态因子图的所有变量配置的模型。这些操作通过构建网格来高效执行，其中每条路径对应于这些变量的特定配置。第 7.2 节集中讨论了因子是参数的非线性函数的模型，而第 7.1 节则重点介绍了因子是线性参数化的更简单的模型。
本节讨论一类称为“图变换器网络” (GTN) 的模型 [LeCun 等人，1998a]。GTN 是为以下情况而设计的：序列结构非常复杂，以至于相应的动态因子图无法明确表示，而必须“程序化”地表示。例如，为了识别整个手写英文句子，必须即时构建因子图，该因子图非常大。相应的网格包含每个语法正确的句子转录的路径，以及每个可能的将句子分割成字符的路径。生成整个网格（或其相关的因子图）是不切实际的，因此必须以程序化方式表示网格。GTN 方法不表示因子图，而是将网格视为机器操作的主要数据结构。GTN 可以看作是一种多层架构，其中的状态是网格，就像神经网络是一种多层架构，其中的状态是固定大小的向量一样。 GTN 可以看作是一个模块网络，称为“图变换器”，它将一个或多个图作为输入并生成另一个图作为输出。大多数模块的操作可以表示为输入图与与模块相关联的另一个图（称为变换器）的组合 [Mohri，1997]。附加到输入图边缘的对象（可以是数字、标签、图像、序列或任何其他实体）被输入到可训练函数，其输出附加到输出图的边缘。由此产生的架构可以看作是一个组合层次结构，其中低级特征和部分通过图组合组合成更高级别的对象。
对于语音识别，声学向量被组合成音素，音素被组合成三音素，三音素被组合成词，词被组合成句子；同样，在手写识别中，墨迹段被组合成字符，字符被组合成词，词被组合成句子。
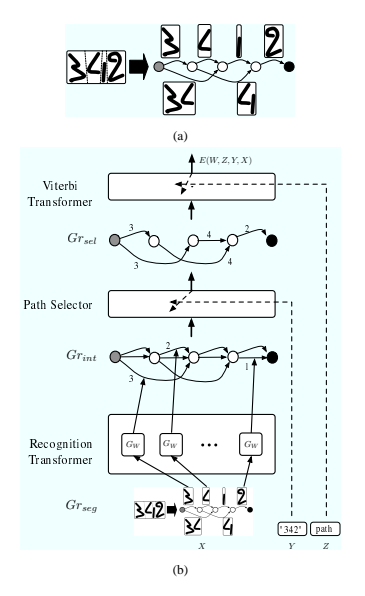
图? 22 显示了用于同时分割和识别手写单词的 GTN 架构示例 [LeCun et al., 1998a]。第一步是对图像进行过度分割并生成分割图（参见@图 22(a)）。
分割图 Grseg 是一个有向无环图 (DAG)，其中从起始节点到终止节点的每条路径都代表将输入图像分割成字符候选的一种特定方式。每个内部节点都与分割产生的候选切口相关联。源节点和目标节点之间的每条弧都与两个切口之间的图像部分相关联。因此，每片墨迹在每条路径上只出现一次。下一阶段将分割图 Grseg 传递给识别转换器，识别转换器生成具有与 Grseg 相同节点数的解释图 Grint。识别转换器包含与判别函数 GW (X) 一样多的相同副本 因为解释图中有弧（这个数字对于每个新输入都会改变）。GW 的每个副本都获取与分割图中一个弧相关联的图像，并在解释图中的相应节点之间生成多个弧。每个输出弧都由字符类别标记，并由将图像分配给该类别的能量加权。因此，解释图中的每条路径代表一种可能的分割输入的一种可能解释，路径上权重的总和代表该解释的组合能量。然后，解释图通过路径选择器模块，该模块仅从解释图中选择具有与 Y（答案）给出的相同标签序列的路径。该模块的输出是另一个称为 Grsel 的图。最后，所谓的维特比变换器选择 Grsel 中由潜在变量 Z 索引的单个路径。Z 的每个值对应于 Grsel 中的不同路径，并且可以解释为输入的特定分割。输出能量可通过最小化或边缘化 Z 获得。最小化 Z 是通过在 Grsel 上运行最短路径算法（例如，维特比算法，因此得名维特比变换器）来实现的。输出能量则是沿最短路径的电弧能量之和。边缘化 Z 是通过在 Grsel 上运行前向算法来实现的，如第 6 节方程 72 所示。路径选择器和维特比变换器可视为特定类型的“开关”模块，它们在其输入图中选择路径。
在[LeCun et al., 1998a]中描述的手写识别系统中，判别函数GW(X)是一个二维卷积网络。这类函数旨在以集成的方式学习低级特征和高级表示，因此在W中是高度非线性的。因此损失函数在W中不是凸的。所提出的优化方法是随机梯度下降的改进版本。
在 [LeCun et al., 1998a] 中，提出了两种训练 GTN 的主要方法： 判别式维特比训练，相当于使用广义感知器损失（等式 7），以及判别式前向训练，相当于使用负对数似然损失（等式 23）。表 1 中的任何良好损失都可以使用。
通过应用以下更新规则，使用随机梯度下降最小化感知器损失来进行训练：
\[W\gets W-\eta\left({\frac{\partial E(W,Y^{i},X^{i})}{\partial W}}-{\frac{\partial E(W,Y^{*i},X^{i})}{\partial W}}\right)。 \tag{86}\]
如何计算 E(W, Y i, Xi) 和 E(W, Y i, Xi) 的梯度？答案很简单，就是将梯度反向传播到整个结构，一直回到判别函数 GW (X)。总能量可以写成以下形式：
\[E(W,Y,X)=\sum_{k l}\delta_{k l}(Y)G_{k l}(W,X), \tag{87}\]
其中总和遍历 Grint 中的所有弧，Gkl(W, X) 是判别函数的第 k 个副本的第 l 个分量，并且如果包含 Gkl(W, X) 的弧存在于最终图中，则 \(\delta_{kl}(Y)\) 是一个二进制值，等于 1，否则等于 0。因此，梯度很简单：
\[{\frac{\partial E(W,Y,X)}{\partial W}}=\sum_{k l}\delta_{k l}(Y){\frac{\partial G_{k l}(W,X)}{\partial W}}. \tag{88}\]
人们必须简单地跟踪\(\delta_{kl}(Y)\)。
在第 5 节中，我们得出结论，广义感知器损失不是一个很好的损失函数。虽然零边距可能会限制解决方案的稳健性，但感知器损失似乎适合作为一种改进系统的方法，该系统已在 [LeCun et al., 1998a] 中建议的分割字符上进行预训练。尽管如此，[LeCun et al., 1998a] 中描述的基于 GTN 的银行支票读取系统已在商业上部署，并使用负对数似然损失进行训练。
训练 GTN 的第二种方法使用 NLL 损失函数，使用公式 72 对 Grsel 的前向算法对 Z 进行边缘化，而不是最小化。
通过应用以下更新规则，使用随机梯度下降最小化 NLL 损失来进行训练：
\[W\gets W-\eta\left(\frac{\partial{\mathcal{F}}_{\mathbb{Z}}(W,Y^{i},X^{i})}{\partial W}-\frac{\partial{\mathcal{F}}_{\mathbb{Y},\mathbb{Z}}(W,X^{i})}{\partial W}\right), \tag{89}\]
在哪里
\[{\mathcal{F}}_{\mathbb{Z}}(W,Y^{i},X^{i})=-{\frac{1}{\beta}}\log\sum_{z\in{\mathcal{Z}}}e^{-\beta E(W,Y^{i},z,X^{i})}, \tag{90}\]
是通过对 Z 进行边缘化而获得的自由能，保持 Xi 和 Yi 不变，并且
\[{\mathcal{F}}_{{\mathcal{Y}},{\mathcal{Z}}}(W,X^{i})=-{\frac{1}{\beta}}\log\sum_{y\in{\mathcal{Y}},\ z\in{\mathcal{Z}}}e^{-\beta E(W,y,z,X^{i})}, \tag{91}\]
是通过对 Y 和 Z 进行边缘化获得的自由能，保持 Xi 不变。计算这些梯度比最小化情况稍微复杂一些。根据链式法则，梯度可以表示为：
\[{\frac{\partial{\mathcal{F}}_{\mathcal{Y},\,\mathcal{Z}}(W,X^{i})}{\partial W}}=\sum_{k l}{\frac{\partial{\mathcal{F}}_{\mathcal{Y},\,\mathcal{Z}}(W,X^{i})}{\partial G_{k l}}}{\frac{\partial G_{k l}(W,X)}{\partial W}}, \tag{92}\]
其中总和遍历解释图中的所有边。第一个因子是通过前向算法（公式 72）获得的量相对于解释图中的一条特定边的导数。这些量可以通过在网格中反向传播梯度来计算，网格被视为具有公式 72 给出的节点函数的前馈网络。我们参考 [LeCun et al., 1998a] 了解详细信息。
与 [Lafferty et al., 2001] 中的说法相反，使用 [LeCun et al., 1998a] 中所述的 NLL 损失训练的 GTN 系统确实为可能的标签序列分配了明确的概率分布。特定解释的概率由公式 46 给出：
\[P(Y|X)=\frac{\int_{z\in\mathcal{Z}}e^{-\beta E(Z,Y,X)}}{\int_{y\in\mathcal{Y},\ z\in\mathcal{Z}}e^{-\beta E(y,z,X)}}. \tag{93}\]
使用广义边际损失之一来训练 GTN 似乎是理所当然的。据我们所知，这从未被做过。
＃＃ 讨论
关于基于能量和概率的模型，仍有一些问题需要回答。本节对这些问题进行了相对哲学的讨论，包括基于能量的推理和学习近似方法的讨论。最后，总结了本章的主要思想。
Ebms 和概率模型
在第 1.3 节中，介绍了通过吉布斯分布将能量转换为概率：
\[P(Y|X,W)={\frac{e^{-\beta E(W,Y,X)}}{\int_{y\in{\mathcal{Y}}}e^{-\beta E(W,y,X)}}}. \tag{94}\]
任何 Y 上的概率分布都可以用该形式的分布任意近似。对于有限能量值，某些 Y 的概率恰好为零的分布只能近似。概率模型的参数估计可以通过多种不同的方式进行，包括使用贝叶斯反演的最大似然估计、最大条件似然估计和（如果可能）贝叶斯平均（可能使用变分近似）。最大化训练样本的条件似然相当于最小化我们所谓的负对数似然损失。
因此，从高层次来看，判别概率模型可以看作是 EBM 的一个特例，其中： - 能量使得积分 Ry∈Y e −βE(W,y,X)(分区函数)收敛。
- 通过最小化负对数似然损失来训练模型。
一个重要的问题涉及概率模型与基于能量的模型的相对优势和劣势。概率模型有两个主要缺点。首先，归一化要求限制了我们可以使用的能量函数的选择。例如，没有理由相信@fig-07中的模型在Y上是可归一化的。事实上，如果函数GW2 (Y ) 有上界，积分 R +∞ −∞ 和 −βE(W,y,X)dy 不收敛。一种常见的解决方法是将一个加法项 Ry(Y ) 添加到能量中，将其解释为 Y 的对数先验，其负指数是可积的。其次，计算负对数似然损失函数中的对比项（或其相对于 W 的梯度）可能非常复杂、昂贵甚至难以解决。各种类型的模型可以分为五个复杂程度不断增加的粗略类别： - 简单：当 Y 是离散的且基数较小时，分区函数是一个包含少量项的总和，可以简单计算。另一个简单情况是分区函数不依赖于 W，因此可以忽略它以进行学习。例如，当 Y 中的能量是具有固定矩阵的二次型时就是这种情况。这些情况下，可以使用能量损失而不必担心崩溃。
解析：当分区函数及其导数可以通过解析计算时。例如，当能量是 Y 中的二次形式，其中矩阵取决于可训练参数时，分区函数是高斯积分（具有可变协方差矩阵），其导数是高斯分布下的期望，两者都有闭式表达式。
可计算：当分区函数是指数项的总和时，但计算可以分解成易于处理的方式。最显著的情况是当分区函数是树型图形模型的输出变量和潜在变量的配置的总和时。在这种情况下，可以使用信念传播来计算分区函数。当图形模型是一个简单的链图（如 HMM 的情况）时，配置集可以用加权网格的路径表示。通过这个网格运行前向算法可以得到分区函数。可以使用一个简单的类似反向传播的过程来计算其梯度（例如，参见 [LeCun et al., 1998a] 及其参考资料）。
可接近：当分区函数无法精确计算，但可以使用各种方法合理地近似时。一个值得注意的例子是当分区函数是循环图形模型配置的总和时。总和无法精确计算，但循环信念传播或其他变分方法可能会产生合适的近似值。有了这些近似值，各种答案的能量仍将被拉高，尽管不像使用完整分区函数那样系统地和具有相同的力。从某种意义上说，变分方法可以在 EBM 的背景下解释 作为选择要拉起的能量子集的一种方法。
难以解决：当分区函数确实难以解决且没有令人满意的变分近似时。在这种情况下，只能使用采样方法。采样方法是一种选择合适候选答案的策略，这些答案的能量将被提升。对此的概率方法是根据答案在模型下的概率对其进行采样，并提升其能量。平均而言，每个答案将根据分区函数被提升适当的量。
在这种情况下，使用基于能量的损失函数（而不是负对数似然函数）可以看作是一种采样方法，该方法具有特定的策略来选择将能量提升的答案。例如，铰链损失系统地选择最令人反感的错误答案作为应将能量提升的答案。最终，使用此类策略将产生能量表面，其中能量差异不能解释为似然比（变分方法也是如此）。我们应该再次强调，如果模型用于预测、分类或决策，这是无关紧要的。
在 EBM 框架中，变分近似方法可以解释为损失函数对比项的特定选择。一种常见的方法是将变分方法和基于能量的损失函数视为概率方法的近似。我们在这里提出的是将概率方法视为更大的基于能量的方法家族的一个特例。基于能量的方法与概率方法同样合理。它们仅用于训练模型来回答与概率模型不同的问题。
一个重要的未决问题是，常用的变分方法（例如，具有流行架构的平均场近似）是否真的满足条件 3（参见第 5.2 节）。
学习效率
影响学习效率的最重要问题是：“在能量表面呈现正确形状之前，必须明确提取多少个错误答案的能量？”基于能量的损失函数会提取最令人讨厌的错误答案，但每次学习迭代时只会提取单个能量。相比之下，负对数似然损失会在每次迭代时提取所有错误答案，包括那些不太可能产生比正确答案更低能量的答案。因此，除非 NLL 计算可以以非常低的成本完成（如“平凡”和“分析”模型的情况），否则基于能量的方法必然会更有效。
一个重要的未决问题是，是否存在替代损失函数，其对比项及其导数比负对数似然损失的计算要简单得多，同时保留了它们提取大量能量“低得令人生畏”的错误答案这一良好特性。也许，可以定义架构和损失函数的品质因数，将评估损失及其导数所需的计算量与能量被提取的错误答案量进行比较。
对于“难以处理”类别的模型，需要上拉或下推的每个能量都需要对能量及其梯度进行评估 （如果使用基于梯度的优化方法）。因此，找到能量表面的参数化，使能量表面以最小的推拉量呈现正确的形状至关重要。如果 Y 是高维的，并且能量表面具有无限的可塑性，那么必须在很多地方拉动能量表面才能使其呈现合适的形状。相反，更“刚性”的能量表面可能以较少的拉力呈现合适的形状，但不太可能接近正确的形状。似乎存在与影响泛化性能的偏差方差困境类似的偏差方差困境。
近似推理学习
很多时候，推理算法只能给出近似答案，或者不能保证给出能量的全局最小值。基于能量的学习在这种情况下能起作用吗？这方面的理论尚不存在，但一些直觉可能会对这个问题有所启发。
Y 中可能存在某些我们的推理算法永远找不到的答案，这可能是因为它们位于算法永远无法到达的空间的遥远区域。我们的模型可能会在这些区域为错误答案赋予较低的能量，但由于推理算法无法找到它们，它们永远不会出现在对比项中，它们的能量也永远不会被提升。幸运的是，由于推理算法找不到这些答案，我们不必担心它们的能量。
基于能量的学习有一个有趣的优势，那就是只有能量被提升的错误答案才真正重要。这与概率损失函数（例如 NLL）形成对比，在概率损失函数中，对比项必须提升每个答案的能量，包括我们的推理算法永远不会找到的答案，这可能会造成浪费。
近似对比样本，对比发散
损失函数的不同之处在于对比样本的选择方式以及其能量提升的程度。一个有趣的建议是提升那些总是接近正确答案的答案，从而使正确答案成为局部最小值，但不一定是全局最小值。这个想法是 Hinton 提出的 对比散度算法 的基础 [Hinton, 2002, Teh et al., 2003]。对比散度学习可以看作是 NLL 学习的近似值，但有两种捷径。首先，通过从分布 P(Y |Xi, W) 中抽取样本来近似等式 24 中的对比项 使用马尔可夫链蒙特卡罗方法。第二步，通过在期望答案处启动马尔可夫链并仅运行链中的几个步骤来挑选样本。
这样就生成了一个接近期望答案的样本 Y˜ i。然后，对参数进行简单的梯度更新：
\[W\gets W-\eta\left(\frac{\partial E(W,Y^{i},X^{i})}{\partial W}-\frac{\partial E(W,\tilde{Y}^{i},X^{i})}{\partial W}\right)。 \tag{95}\]
由于对比样本总是接近期望答案，因此可以希望期望答案会成为能量的局部最小值。仅运行几步 MCMC 可以限制计算成本。但是，并不能保证所有能量低的错误答案都会被提取出来。
＃＃＃ 结论
本教程旨在介绍和阐述以下主要思想： - 许多现有的学习模型可以用基于能量的学习框架来简单地表达。
在文献中提出的许多损失函数中，有些是好的（具有非零边际），有些则可能不好。
概率学习是基于能量的学习的一个特例，其中损失函数是负对数似然，又名最大互信息准则。
使用随机梯度方法优化损失函数通常比黑箱凸优化方法更有效。
随机梯度法可应用于任何损失函数，包括非凸函数。由于空间的维数较高，局部最小值在实践中很少成为问题。
支持向量马尔可夫模型、最大边际马尔可夫网络和条件随机场都是使用线性参数化能量因子的序列建模系统。自 20 世纪 90 年代初以来，用于语音和手写识别的非线性参数化序列建模系统一直是一个非常活跃的研究领域。
图形变换器网络是分层序列建模系统，其中操纵的对象是包含给定级别所有替代解释的网格。可以使用随机梯度进行全局训练，方法是使用一种反向传播算法来计算系统中所有参数的损失梯度。
致谢
作者感谢 Geoffrey Hinton、Leon Bottou、Yoshua Bengio、Sebastian Seung 和 Brendan Frey 的有益讨论。
这项工作部分由 NSF ITR 拨款 0325463“预测学习的新方向”资助。
参考文献
[Altun and Hofmann, 2003] Altun, Y. and Hofmann, T. (2003). Large margin methods for label sequence learning. In Proc. of 8th European Conference on Speech Communication and Technology (EuroSpeech).
[Altun et al., 2003] Altun, Y., Johnson, M., and Hofmann, T. (2003). Loss functions and optimization methods for discriminative learning of label sequences. In Proc. EMNLP.
[Bahl et al., 1986] Bahl, L., Brown, P., de Souza, P., and Mercer, R. (1986). Maximum mutual information estimation of hidden markov model parameters for speech recognition. In Proceedings of Acoustics, Speech, and Signal Processing Conference, pages 49–52.
[Becker and LeCun, 1989] Becker, S. and LeCun, Y. (1989). Improving the convergence of back-propagation learning with second-order methods. In Touretzky, D., Hinton, G., and Sejnowski, T., editors, Proc. of the 1988 Connectionist Models Summer School, pages 29–37, San Mateo. Morgan Kaufman.
[Bengio, 1996] Bengio, Y. (1996). Neural Networks for Speech and Sequence Recognition. International Thompson Computer Press, London, UK.
[Bengio et al., 1990] Bengio, Y., Cardin, R., De Mori, R., and Normandin, Y. (1990). A hybrid coder for hidden markov models using a recurrent network. In Proceeding of ICASSP, pages 537–540.
[Bengio et al., 1992] Bengio, Y., De Mori, R., Flammia, G., and Kompe, R. (1992). Global optimization of a neural network-hidden Markov model hybrid. IEEE Transaction on Neural Networks, 3(2):252–259.
[Bengio et al., 1991] Bengio, Y., DeMori, R., Flammia, G., and Kompe, R. (1991). Global optimization of a neural network - hidden markov model hybrid. In Proceedings of EuroSpeech’91.
[Bengio et al., 2003] Bengio, Y., Ducharme, R., Vincent, P., and Jauvin, C. (2003). A neural probabilistic language model. Journal of Machine Learning Research, 3:1137–1155.
[Bengio and Frasconi, 1996] Bengio, Y. and Frasconi, P. (1996). An input/output HMM architecture. In Tesauro, G., Touretzky, D., and Leen, T., editors, Advances in Neural Information Processing Systems, volume 7, pages 427–434. MIT Press, Cambridge, MA.
[Bengio et al., 1993] Bengio, Y., LeCun, Y., and Henderson, D. (1993). Globally trained handwritten word recognizer using spatial representation, space displacement neural networks and hidden markov models. In Cowan, J. and Tesauro, G., editors, Advances in Neural Information Processing Systems, volume 6. Morgan Kaufmann.
[Bengio et al., 1995] Bengio, Y., LeCun, Y., Nohl, C., and Burges, C. (1995). Lerec: A nn/hmm hybrid for on-line handwriting recognition. Neural Computation, 7(6):1289–1303.
[Bottou, 1991] Bottou, L. (1991). Une Approche theorique de l’Apprentissage Con- ´ nexionniste: Applications a la Reconnaissance de la Parole ` . PhD thesis, Universit´e de Paris XI, 91405 Orsay cedex, France.
[Bottou, 2004] Bottou, L. (2004). Stochastic learning. In Bousquet, O. and von Luxburg, U., editors, Advanced Lectures on Machine Learning, number LNAI 3176 in Lecture Notes in Artificial Intelligence, pages 146–168. Springer Verlag, Berlin.
[Bottou and LeCun, 2004] Bottou, L. and LeCun, Y. (2004). Large-scale on-line learning. In Advances in Neural Information Processing Systems 15. MIT Press.
[Bottou et al., 1997] Bottou, L., LeCun, Y., and Bengio, Y. (1997). Global training of document processing systems using graph transformer networks. In Proc. of Computer Vision and Pattern Recognition, pages 490–494, Puerto-Rico. IEEE.
[Bourlard and Morgan, 1990] Bourlard, H. and Morgan, N. (1990). A continuous speech recognition system embedding mlp into hmm. In Touretzky, D., editor, Advances in Neural Information Processing Systems 2, pages 186–193. Morgan Kaufmann.
[Bromley et al., 1993] Bromley, J., Guyon, I., LeCun, Y., Sackinger, E., and Shah, R. (1993). Signature verification using a siamese time delay neural network. In Cowan, J. and Tesauro, G., editors, Advances in Neural Information Processing Systems, volume 6. Morgan Kaufmann.
[Chopra et al., 2005] Chopra, S., Hadsell, R., and LeCun, Y. (2005). Learning a similarity metric discriminatively, with application to face verification. In Proc. of Computer Vision and Pattern Recognition Conference. IEEE Press.
[Collins, 2000] Collins, M. (2000). Discriminative reranking for natural language parsing. In Proceedings of ICML 2000.
[Collins, 2002] Collins, M. (2002). Discriminative training methods for hidden markov models: Theory and experiments with perceptron algorithms. In Proc. EMNLP.
[Collobert et al., 2006] Collobert, R., Weston, J., and Bottou, L. (2006). Trading convexity for scalability. In Proceedings of the Twenty-third International Conference on Machine Learning (ICML 2006). IMLS/ICML. ACM Digital Library.
[Denker and Burges, 1995] Denker, J. S. and Burges, C. J. (1995). Image segmentation and recognition. In The Mathematics of Induction. Addison Wesley.
[Driancourt, 1994] Driancourt, X. (1994). *Optimisation par descente de gradient stochastique de systemes modulaires combinant reseaux de neurones et programmation dynamique. Application a la reconnaissance de la parole. (optimization through stochastic gradient of modular systems that combine neural networks and dynamic programming, with applications to speech recognition). PhD thesis, Universit´e de Paris XI, 91405 Orsay cedex, France.
[Driancourt et al., 1991a] Driancourt, X., Bottou, L., and Gallinari, P. (1991a). MLP, LVQ and DP: Comparison & cooperation. In Proceedings of the International Joint Conference on Neural Networks, volume 2, pages 815–819, Seattle.
[Driancourt et al., 1991b] Driancourt, X., Bottou, L., and P., G. (1991b). Comparison and cooperation of several classifiers. In Proceedings of the International Conference on Artificial Neural Networks (ICANN).
[Driancourt and Gallinari, 1992a] Driancourt, X. and Gallinari, P. (1992a). Empirical risk optimisation: neural networks and dynamic programming. In Proceedings of Neural Networks for Signal Processing (NNSP).
[Driancourt and Gallinari, 1992b] Driancourt, X. and Gallinari, P. (1992b). A speech recognizer optimaly combining learning vector quantization, dynamic programming and multi-layer perceptron. In Proceedings of ICASSP.
[Franzini et al., 1990] Franzini, M., Lee, K. F., and Waibel, A. (1990). Connectionnist viterbi training: A new hybrid method for continuous speech recognition. In Proceedings of ICASSP, page 245.
[Hadsell et al., 2006] Hadsell, R., Chopra, S., and LeCun, Y. (2006). Dimensionality reduction by learning an invariant mapping. In Proc. Computer Vision and Pattern Recognition Conference (CVPR’06). IEEE Press.
[Haffner, 1993] Haffner, P. (1993). Connectionist speech recognition with a global MMI algorithm. In EUROSPEECH’93, 3rd European Conference on Speech Communication and Technology, Berlin.
[Haffner et al., 1991] Haffner, P., Franzini, M., and Waibel, A. H. (1991). Integrating time-alignment and neural networks for high performance continuous speech recognition. In Proceeding of ICASSP, pages 105–108. IEEE.
[Haffner and Waibel, 1991] Haffner, P. and Waibel, A. H. (1991). Time-delay neural networks embedding time alignment: a performance analysis. In EUROSPEECH’91, 2nd European Conference on Speech Communication and Technology, Genova, Italy.
[Haffner and Waibel, 1992] Haffner, P. and Waibel, A. H. (1992). Multi-state timedelay neural networks for continuous speech recognition. In Advances in Neural Information Processing Systems, volume 4, pages 579–588. Morgan Kaufmann, San Mateo.
[Hinton, 2002] Hinton, G. E. (2002). Training products of experts by minimizing contrastive divergence. Neural Computation, 14:1771–1800.
[Huang and LeCun, 2006] Huang, F.-J. and LeCun, Y. (2006). Large-scale learning with svm and convolutional nets for generic object categorization. In Proc. Computer Vision and Pattern Recognition Conference (CVPR’06). IEEE Press.
[Juang et al., 1997] Juang, B.-H., Chou, W., and Lee, C.-H. (1997). Minimum classification error rate methods for speech recognition. IEEE Transactions on Speech and Audio Processing, 5(3):257–265.
[Konig et al., 1996] Konig, Y., Bourlard, H., and Morgan, N. (1996). REMAP: Recursive estimation and maximization of A posteriori probabilities - application to transition-based connectionist speech recognition. In Touretzky, D. S., Mozer, M. C., and Hasselmo, M. E., editors, Advances in Neural Information Processing Systems, volume 8, pages 388–394. The MIT Press.
[Kschischang et al., 2001] Kschischang, F., Frey, B., and Loeliger, H.-A. (2001).
Factor graphs and the sum-product algorithm. IEEE Trans. Information Theory, 47(2):498–519.
[Kumar and Hebert, 2004] Kumar, S. and Hebert, M. (2004). Discriminative fields for modeling spatial dependencies in natural images. In Thrun, S., Saul, L., and Sch¨olkopf, B., editors, Advances in Neural Information Processing Systems 16. MIT Press, Cambridge, MA.
[Lafferty et al., 2001] Lafferty, J., McCallum, A., and Pereira, F. (2001). Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proc. International Conference on Machine Learning (ICML).
[LeCun and Bengio, 1994] LeCun, Y. and Bengio, Y. (1994). word-level training of a handwritten word recognizer based on convolutional neural networks. In IAPR, editor, Proc. of the International Conference on Pattern Recognition, volume II, pages 88–92, Jerusalem. IEEE.
[LeCun et al., 1997] LeCun, Y., Bottou, L., and Bengio, Y. (1997). Reading checks with graph transformer networks. In International Conference on Acoustics, Speech, and Signal Processing, volume 1, pages 151–154, Munich. IEEE.
[LeCun et al., 1998a] LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998a).
Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324.
[LeCun et al., 1998b] LeCun, Y., Bottou, L., Orr, G., and Muller, K. (1998b). Efficient backprop. In Orr, G. and K., M., editors, Neural Networks: Tricks of the trade. Springer.
[LeCun and Huang, 2005] LeCun, Y. and Huang, F. (2005). Loss functions for discriminative training of energy-based models. In Proc. of the 10-th International Workshop on Artificial Intelligence and Statistics (AIStats’05).
[Ljolje et al., 1990] Ljolje, A., Ephraim, Y., and Rabiner, L. R. (1990). Estimation of hidden markov model parameters by minimizing empirical error rate. In Proc. of International Conference on Acoustics, Speech, and Signal Processing, pages 709– 712.
[MacKay, 2003] MacKay, D. J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press. Available from http://www.inference.phy.cam.ac.uk/mackay/itila/.
[McCallum et al., 2000] McCallum, A., Freitag, D., and Pereira, F. (2000). Maximum entropy markov models for information extraction and segmetnation. In Proc. International Conference on Machine Learning (ICML), pages 591–598.
[McDermott, 1997] McDermott, E. (1997). Discriminative Training for Speech Recognition. PhD thesis, Waseda University.
[McDermott and Katagiri, 1992] McDermott, E. and Katagiri, S. (1992). Prototypebased discriminative training for various speech units. In Proceedings of ICASSP92, San Francisco, CA, USA, pages 417–420.
[Mohri, 1997] Mohri, M. (1997). Finite-state transducers in language and speech processing. Computational Linguistics, 23(2):269–311.
[Morgan and Bourlard, 1995] Morgan, N. and Bourlard, H. (1995). Continuous speech recognition: An introduction to the hybrid hmm/connectionist approach. IEEE Signal Processing Magazine, 12(3):25–42.
[Ning et al., 2005] Ning, F., Delhomme, D., LeCun, Y., Piano, F., Bottou, L., and Barbano, P. (2005). Toward automatic phenotyping of developing embryos from videos. IEEE Transactions on Image Processing, 14(9):1360–1371. Special issue on Molecular and Cellular Bioimaging, to appear.
[Osadchy et al., 2005] Osadchy, R., Miller, M., and LeCun, Y. (2005). Synergistic face detection and pose estimation with energy-based model. In Advances in Neural Information Processing Systems (NIPS 2004). MIT Press.
[Sakoe et al., 1988] Sakoe, H., Isotani, R., Yoshida, K., Iso, K., and Watanabe, T. (1988). Speaker-independant word recognition using dynamic programming neural networks. In Proceedings of ICASSP-88, New York, pages 107–110.
[Solla et al., 1988] Solla, S., Levin, E., and Fleisher, M. (1988). Accelerated learning in layered neural networks. Complex Systems, 2(6):625–639.
[Taskar et al., 2003] Taskar, B., Guestrin, C., and Koller, D. (2003). Max-margin markov networks. In Proc. NIPS.
[Teh et al., 2003] Teh, Y. W., Welling, M., Osindero, S., and E., H. G. (2003). Energybased models for sparse overcomplete representations. Journal of Machine Learning Research, 4:1235–1260.
[Vapnik, 1995] Vapnik, V. (1995). The Nature of Statistical Learning Theory. Springer Verlag.
[Vishwanathan et al., 2006] Vishwanathan, S. V. N., Schraudolph, N. N., Schmidt, M. W., and Murphy, K. P. (2006). Accelerated training of conditional random fields with stochastic gradient methods. In Proceedings of the Twenty-third International Conference on Machine Learning (ICML 2006). IMLS/ICML.
[Yedidia et al., 2005] Yedidia, J., Freeman, W., and Weiss, Y. (2005). Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Transactions on Information Theory, 51(7):2282–2312.