译者按
本文为 Eero P Simoncelli 经典论文《Natural Image Statistics And Neural Representation》的中文翻译，目标是为了更好的学习这一篇经典著作。
如果需要有更好的阅读体验，也可以阅读本文的 PDF 版本，对排版、翻译的质量问题，可在本文中留言或标记，也可邮件联系本人进行处理：linxuhong@yahoo.com
介绍
了解神经元和神经系统的功能是系统神经科学的主要目标。此类系统的进化和发展由三个基本因素驱动：(a) 生物体必须执行的任务，(b) 神经元的计算能力和局限性（这包括代谢和布线限制），以及 (c) 生物体所处的环境。神经处理的理论研究和模型受前两个因素的影响最大。但最近更强大的自然环境模型的发展引起了人们对环境在确定神经计算结构方面的作用的兴趣。
这种生态约束的使用在感觉系统中最为明显，长期以来人们一直认为神经元在进化、发育和行为的时间尺度上会适应它们所接触的信号。由于并非所有信号都具有相同的可能性，因此人们自然而然地认为感知系统应该能够最好地处理那些最常出现的信号。因此，环境的统计特性与感觉处理有关。这些概念是工程学科的基础：源编码、估计和决策理论都严重依赖于环境的统计“先验”模型。
建立环境统计和神经处理之间的精确定量关系非常重要，原因有很多。除了提供理解神经元功能特性的框架外，这种关系还可以导致基于环境统计推导新的计算模型。它还可以用于设计新形式的随机实验方案和用于探索生物系统的刺激。最后，它可以导致与人类交互的设备设计的根本性改进。
尽管人们普遍认为神经处理必定受到环境统计数据的影响，但要使这种联系在数量上精确起来却出奇地困难。40 多年前，受信息理论发展的推动，Attneave (1954) 提出视觉感知的目标是产生对传入信号的有效表示。在神经生物学背景下，Barlow (1961) 假设早期感觉神经元的作用是消除感觉输入中的统计冗余。许多其他作者也提出了这种“有效编码”假设的变体（例如 Laughlin 1981、Atick 1992、van Hateren 1992、Field 1994、Riecke 等人 1995）。
但即使给出了这样的联系，假设也未完全明确。还需要说明哪种环境塑造了系统。从数量上讲，这意味着在输入信号空间上指定概率分布。因为这本身就是一个难题，所以许多作者的研究基于从代表相关环境的大量示例图像中计算出的经验统计数据。此外，还必须指定环境塑造系统的时间尺度。最后，需要说明哪些神经元应该满足效率标准，以及如何解释它们的反应。
有两种基本方法可以测试和改进这种感觉处理假设。更直接的方法是检查自然刺激条件下神经反应的统计特性（例如 Laughlin 1981、Rieke 等人 1995、Dan 等人 1996、Baddeley 等人 1998、Vinje 和 Gallant 2000）。另一种方法是“推导”早期感觉处理的模型（例如 Sanger 1989、Foldiak 1990、Atick 1992、Olshausen 和 Field 1996、Bell 和 Sejnowski 1997、van Hateren 和 van der Schaaf 1998、Simoncelli 和 Schwartz 1999）。在这种方法中，人们检查环境信号的统计特性，并表明根据某些统计优化标准得出的变换可以很好地描述一组感觉神经元的反应特性。在以下章节中，我们将回顾将环境统计数据与神经处理联系起来的基本概念框架，并讨论一系列示例，其中作者使用上述两种方法之一来为这种联系提供证据。
基本概念
信息理论是二十世纪的一项根本性发展。香农 (1948) 提出了这一理论，目的是量化和解决通信信道中传输信号的问题。但他提出的信息定量测量公式超越了任何特定的应用、设备或算法，并成为信息获取、传输、处理和存储方面大量科学知识和工程发展的基础。事实上，它本质上已成为一种信号计算理论。
因此，信息论在神经系统的建模和理解中起着根本性的作用。神经科学研究人员一直对神经元数量明显激增感到困惑，因为要唯一地表示可能遇到的每个视觉（或其他感官）模式，需要的神经元数量会激增。Barlow（1961）认识到信息论在这种背景下的重要性，并提出神经处理的一个重要制约因素是信息（或编码）效率。也就是说，一组神经元应该编码尽可能多的信息，以便最有效地利用可用的计算资源。我们很快就会对此进行更精确的阐述，但首先有几点值得一提。
神经代码的效率既取决于将输入映射到神经响应的转换，也取决于输入的统计数据。特别是，一个输入集合的神经响应的最佳效率并不意味着优于其他输入集合！
有效编码原则不应与最佳压缩（即速率失真理论）或最佳估计相混淆。特别是，它没有提到信号表示的准确性，也不要求从输入到神经反应的转换是可逆的。这可以被视为一种优势（因为不需要考虑任何关于表示形式的假设，也不需要考虑错误表示输入的成本）或限制（因为这些成本显然与真实生物有关）。
上面给出的简单有效编码标准没有提到可能污染输入刺激的噪声。它也没有提到对相同刺激的神经反应的不确定性或可变性。也就是说，它假设神经反应与输入信号具有确定性关系。如果这些外部和内部噪声源与刺激和神经反应相比较小，则所述标准近似为最优。但更完整的解决方案应该考虑噪声，通过最大化反应提供的有关刺激的信息（技术上讲，刺激和反应之间的相互信息）。这个量通常很难测量，但 Bialek 等人（1991 年）和 Rieke 等人（1995 年）最近开发了近似技术来估计它。
如果有效编码假设是正确的，那么我们应期望在神经元的响应特性中看到哪些行为？这个问题的答案可以巧妙地分为两个相关部分：单个神经响应的分布形状和神经元之间的统计依赖性。
单个神经元中的高效编码
考虑单个神经元对某些自然环境的反应活动分布。1 为了确定该神经元传达的信息是否最大，我们需要对响应值施加约束（如果它们可以取任何实值，则可以编码的信息量是无限的）。例如，假设我们假设响应被限制为某个最大值 R_max 。很容易看出，传达最大信息的响应分布在区间 [0, R_max] 上是均匀的。也就是说，高效的神经元应该平等地利用其所有可用的响应级别。最佳分布主要取决于神经响应约束。例如，如果选择方差固定的替代约束，则信息最大化响应分布为高斯分布。类似地，如果响应的平均值是固定的，则信息最大化响应分布是指数的。2
在多个神经元中高效编码
如果一组神经元共同编码有关刺激的信息，那么有效编码假设要求每个神经元的反应都是最佳的，如上所述。此外，如果对任何特定信息进行编码的努力在多个神经元中重复，则编码不可能有效。类似于单一反应情况背后的直觉，联合反应应该平等地利用所有可能的响应水平组合。从数学上讲，这意味着神经反应必须在统计上独立。这种代码通常称为因子代码，因为神经反应的联合概率分布可以分解为各个响应概率分布的乘积。一组神经反应的独立性也意味着人们无法通过观察该组中其他神经元的反应来了解任何一个神经元的反应。换句话说，给定其他神经元的反应，一个神经元的反应的条件概率分布应该是固定分布（即不应依赖于其他神经元的反应水平）。独立性的优点在于，与单个神经元的结果不同，它不需要任何辅助约束。
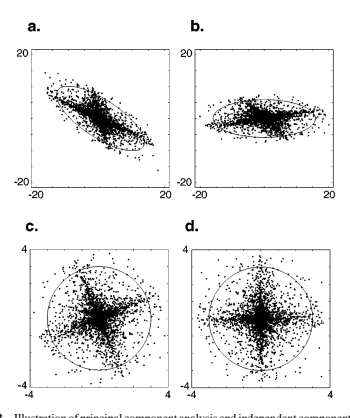
现在考虑最佳传感系统“设计师”面临的问题。设计师希望将输入信号分解为一组独立的响应。这个一般问题极其困难，因为表征输入的联合直方图会随着维数的增加而呈指数增长，因此通常必须通过简化输入统计数据的描述和/或限制分解形式来限制问题。最著名的限制是仅考虑线性分解，并且仅考虑输入信号的二阶（即协方差或等效相关性）属性。可以使用一种称为主成分分析 (PCA)3的优雅且易于理解的技术来找到此问题的解。主成分是一组正交轴，各成分沿这些轴去相关。这样的一组轴始终存在，尽管它不必是唯一的。
如果数据按照多维高斯分布4，那么这些轴所表示的数据分量在统计上是独立的。
这在 Figure 1 中针对二维源（例如双像素图像）进行了说明。
将数据集转换到主成分坐标系后，通常会重新调整空间的轴以均衡每个成分的方差（通常将它们设置为 1）。此重新调整过程通常称为“白化”，如 Figure 1 所示。
当将 PCA 应用于图像等信号时，通常假设图像的统计特性是平移不变的（也称为平稳的）。具体而言，假设图像中两个位置的强度相关性仅取决于位置之间的位移，而不取决于它们的绝对位置。在这种情况下，傅里叶变换的正弦基函数保证是一组有效的主成分轴（尽管与以前一样，该组不必是唯一的）。沿每个轴的方差只是傅里叶功率谱。白化可以通过计算傅里叶变换、将每个频率分量除以其方差的平方根以及（可选）计算逆傅里叶变换来实现。这将在下文进一步讨论。
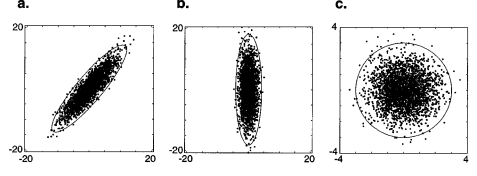
尽管 PCA 可用于恢复一组统计上独立的轴以表示高斯数据，但当数据为非高斯数据时，该技术通常会失败。作为一个简单的例子，考虑从两个独立的非高斯源的线性混合源中提取的数据（Figure 2）。非高斯性在沿两个斜轴延伸的数据长尾中显而易见。Figure 2 还显示了主成分轴和白化数据的旋转。请注意，白化数据的轴与空间的轴不对齐。特别是，在数据是非高斯源的线性混合的情况下，可以证明需要额外旋转坐标系才能恢复原始的独立轴。5 但只能通过查看协方差以外的数据统计属性（即高于二阶）来估计适当的旋转。
在过去十年中，许多研究人员已经开发出估算最终旋转矩阵的技术（例如 Cardoso 1989、Jutten & Herauult 1991、Comon 1994）。这些算法通常最大化高阶矩（例如峰度，即四阶矩除以二阶矩的平方），而不是直接优化轴分量的独立性。这种分解通常称为独立分量分析 (ICA)，虽然这有点用词不当，因为除非原始源实际上是具有较大高阶矩（例如重尾）的源的线性混合，否则无法保证所得分量是独立的。尽管如此，人们通常可以使用这种技术来恢复数据最独立的线性轴。6幸运的是，这种方法在图像的情况下非常成功（见下文）。
图像统计：案例研究
自然图像在统计上是冗余的。许多作者指出，在所有可能的视觉图像中，我们只能看到很小一部分（例如 Attneave 1954、Field 1987、Daugman 1989、Ruderman & Bialek 1994）。Kersten（1987） 通过要求人类受试者替换四位数字图像中缺失的像素，从感知上证明了这种冗余。然后，他使用正确猜测的百分比来估计像素的感知信息内容约为 1.4 位 [Shannon (1948) 使用类似的技术来估计书面英语的冗余度]。现代技术每天都在利用这种冗余来传输和存储压缩格式的数字化图像。
在以下章节中，我们将描述图像的各种统计特性及其与视觉处理的关系。
强度统计
最简单的统计图像描述是视觉场景中光强度的分布。如上一节所述，有效编码假设预测单个神经元应最大化信息传输。为了很好地证实这一想法，Laughlin（1981）发现苍蝇视觉系统中大单极细胞的对比度响应函数大致满足最佳编码标准。具体来说，他测量了苍蝇环境中对比度的概率分布，并表明该分布通过对比度与神经元膜电位相关的函数近似地转换为均匀分布。Baddeley 等人（1998）表明，猫和猴子的初级和下颞视觉皮层中脉冲神经元的瞬时发放率呈指数分布（当受到自然场景的视觉刺激时），这与对平均发放率有限制的最佳编码一致。
颜色统计
除了强度之外，落在图像上特定位置的光还具有光谱（波长）分布。人类视觉系统的视锥细胞将这种分布表示为三维量。Buchsbaum & Gottshalk (1984) 假设自然界中经历的波长光谱可以很好地近似为由视锥细胞光谱敏感性所形成的三维子空间。Maloney (1986) 研究了自然界中反射函数的经验分布，不仅表明它可以通过低维空间很好地表示，而且表面反射率估计问题实际上可以通过视锥细胞的光谱敏感性进行过滤来辅助解决。
另一种方法是假设视锥细胞的光谱敏感度构成固定的波长前端分解，并询问应对它们的响应执行哪些处理。Ruderman 等人 (1998) 在 Buchsbaum 和 Gottschalk (1983) 先前工作的基础上，研究了对大量树叶高光谱摄影图像的对数视锥细胞响应的统计特性。对数的使用大致受到心理物理原理 (韦伯-费希纳定律) 的启发，并作为分布的对称化运算。他们发现数据集的主成分轴沿着对应于 {L+M+S, L+M−2S, L−M} 的方向，其中 {L,M,S} 对应于长、中、短波长视锥细胞的对数响应。尽管这些轴与感知和生理测量的“对手”机制的相似性很有趣，但这些机制的确切形式取决于用于测量它们的实验（参见 Lennie & D’Zmura 1988）。
空间相关性
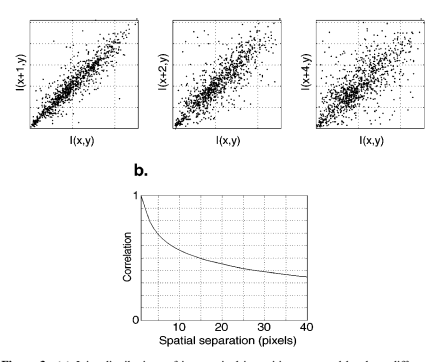
即使只是随意检查一下自然图像，也可以看出相邻的空间位置在强度上是高度相关的。Figure 3 证明了这一点，它显示了强度值对的散点图，这些强度值由三个不同的距离分隔开，并对几个不同的自然图像的绝对位置取平均值。总结这些依赖关系的标准测量是自相关函数 \(C(\Delta x,\Delta y)\)，它给出了两个位置的强度与相对位置的相关性（乘积的平均值）。从 Figure 3 中的例子可以看出，相关性的强度随着距离的增加而下降。7
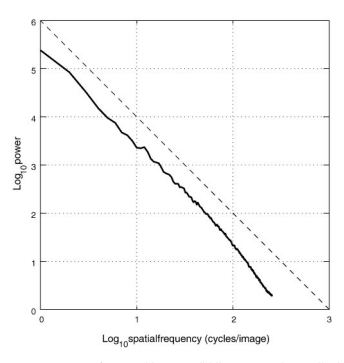
通过计算相对分离函数的相关性，我们假设图像中的空间统计是平移不变的。如上所述，平移不变性的假设意味着可以通过变换到频率（傅里叶）域来去相关图像。然后可以通过在二维傅里叶平面内执行旋转平均将二维功率谱简化为空间频率的一维函数。根据经验，许多作者发现自然图像的光谱功率随频率 \(f\) 下降，符合幂律 \(1/f^p\)，p 的估计值通常接近 2 [请参阅 Tolhurst (1992) 或 Ruderman & Bialek (1994) 的评论]。示例如 Figure 4 所示。
这种幂律行为的环境原因一直是人们猜测和争论的主题。最普遍的观点之一是，这是由于视觉世界的尺度不变性造成的。尺度不变性意味着，如果改变观察的尺度，图像的统计特性不应改变。特别是，功率谱在这种重新缩放下不应改变形状。将图像的坐标在空间上重新缩放 \(\text{a}\) 倍会导致将相应的傅立叶域轴重新缩放 \(1/\alpha\) 倍。只有服从幂律的傅立叶谱才会在这种变换下保持其形状。另一个常见的理论是，\(1/f^{2}\) 功率谱是由于图像中存在边缘，因为边缘本身具有 \(1/f^2\) 功率谱。然而，Ruderman (1997) 和 Lee & Mumford (1999) 认为，自然图像中物体的大小和距离的特定分布决定了光谱衰减。
视觉系统是否利用了自然图像的相关结构？Srinivasan 等人 (1982) 首次定量研究了这个问题。他们测量了自然场景的自相关函数，然后计算了邻近光感受器需要多少减法抑制才能有效抵消这些相关性。然后，他们将预测的抑制周围场与苍蝇复眼中一级中间神经元实际测量的抑制周围场进行了比较。这种对应关系出奇地好，为早期空间视觉处理中的去相关提供了第一个定量证据。
Atick & Redlich (1991, 1992) 将这种分析进一步推进，他们考虑了在存在白色光感受器噪声的情况下，自然图像功率谱的白化问题（相当于去相关）。他们表明，单细胞生理学和心理物理测量的对比敏感度函数都与白化滤波器和用于消除噪声的最佳低通滤波器（称为维纳滤波器）的乘积一致。van Hateren (1992) 对苍蝇视觉系统做出了类似的预测和生理比较。加入维纳滤波器允许系统的行为随平均亮度水平而变化。具体而言，在较低的亮度水平（因此信噪比较低）下，滤波器变得更低通（直观地说，在更大的空间区域上取平均值以恢复较弱的信号）。Balboa & Grzywacz (2000) 提出了一种有趣的视网膜水平细胞替代模型。他们假设了一种视网膜周围抑制的分裂形式，并表明在存在光子吸收噪声的情况下，有效感受野大小的变化对于强度边缘的表示是最佳的。
高阶统计
高效编码假设与视网膜神经处理之间的一致性令人鼓舞，但高效编码假设对皮质处理有何看法？许多研究人员（例如 Sanger 1989、Hancock 等人 1992、Shonual 等人 1997）利用自然图像的协方差特性来推导线性基函数，这些函数类似于生理上在初级视觉皮层中发现的感受野（即定向带通滤波器）。但这些需要额外的约束，例如空间局部性和/或对称性，以实现近似皮质感受野的函数。
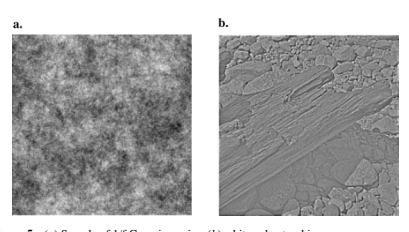
如介绍中所述，PCA 仅基于二阶（协方差）统计数据，如果源分布为非高斯分布，则可能会失败。有多种方法可以发现自然图像的分布为非高斯分布。首先，我们应该能够通过生成一组独立的高斯傅里叶系数（即高斯白噪声）、对这些系数进行反白化（乘以 \(1/f^{2}\)）然后反转傅里叶变换来从图像分布中抽取样本。
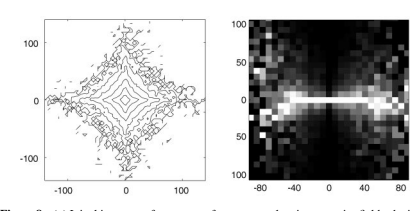
Figure 5 a 中显示了这样的图像。请注意，它没有任何边缘、轮廓或我们期望在自然场景中找到的许多其他结构。其次，如果它是高斯的（并且平移不变），那么傅里叶变换应该使分布去相关，而白化应该产生独立的高斯系数（参见 Figure 5）。但是白化的自然图像仍然包含明显的结构（即线条、边缘、轮廓等），如 Figure 5 b 所示。因此，即使通过白化消除了视网膜和外侧膝状体中的相关性，在有效编码自然图像方面仍有许多工作要做。
Field (1987) 和 Daugman (1989) 提供了自然图像非高斯性的更多直接证据。他们指出，定向带通滤波器（例如 Gabor 滤波器）的响应分布在零处具有尖锐的峰值，并且尾部比高斯密度长得多（参见 Figure 6）。由于多维高斯分布沿任何轴的密度也必须是高斯的，因此这构成了直接 Figure 6 Gabor 滤波器对自然图像的响应直方图，与相同方差的高斯分布相比。
证据表明整体密度不能服从高斯分布。Field (1987) 认为，对应于这些密度的表示（其中大多数神经元具有小幅度响应）具有重要的神经编码特性，他称之为稀疏性。通过对 Gabor 函数的参数进行优化 （空间频率带宽和纵横比），他表明产生最小显著系数分数的参数与皮质简单细胞中发现的响应特性范围很好地匹配（即带宽为 0.5-1.5 个八度，纵横比为 1-2）。
Olshausen & Field (1996; 1997) 重新审视了简单细胞感受野与稀疏编码之间的关系，但没有对感受野施加特定的函数形式。他们基于基函数的线性叠加创建了一个图像模型，并调整了这些函数，以最大限度地提高表示的稀疏性（系数为零的基函数数量），同时保留图像中的信息（通过保持均方重建误差的界限）。在对从自然场景中随机提取的数十万个图像块进行训练后出现的函数集，从完全随机的初始条件开始，与简单细胞的空间感受野属性非常相似 - 即它们在不同的空间频带中具有空间局部性、方向性和带通性（Figure 7）。这种方法也可以重新定义为一个概率模型，该模型试图用既稀疏又统计独立的成分来解释图像（Olshausen & Field 1997），因此是更广泛的 ICA 算法类别的成员（见上文）。使用其他形式的 ICA（Bell & Sejnowski 1997、van Hateren & van der Schaaf 1998、Lewicki & Olshausen 1999）也获得了类似的结果，Hyvärinen &Hoyer（2000）通过扩展 ICA 以在子空间上进行操作，得出了复杂的细胞特性。从生理学上讲，Vinje & Gallant（2000）表明，在呈现自然场景刺激时，初级视觉皮层神经元的反应更加稀疏。
需要注意的是，尽管这些技术寻求统计独立性，但最终的响应实际上从来都不是完全独立的。原因是这些模型仅限于以线性叠加的方式描述图像，但图像并非由独立成分的总和形成。例如，考虑这样一个事实：来自不同物体的光在图像形成过程中通常根据遮挡规则（而不是相加）组合。对这些统计关系形式的分析揭示了跨空间以及跨尺度和方向的非线性依赖关系（Wegmann & Zetzche 1990、Simoncelli 1997、Simoncelli & Schwartz 1999）。
考虑由两个不重叠的线性感受野的响应形成的联合直方图，如 Figure 8 a 所示。直方图清楚地表明数据与轴对齐，就像上面描述的独立成分分解一样。但从这张图片中无法判断响应是否独立。请考虑 Figure 8 b 的条件直方图。每列给出纵坐标变量 r_2 的概率分布，假设横坐标变量 r_1 的对应值。也就是说，数据与 Figure 8 a 中的数据相同，只是每列都已独立标准化。条件直方图说明了两个响应之间关系的几个重要方面。首先，它们（大约）不相关：通过数据的最佳拟合回归线是通过原点的零斜率线。但它们显然不独立，因为 r2 的方差表现出对 r1 值的强烈依赖。因此，虽然r2与r1不相关，但从统计上看，它们仍然是相关的，而且这种相关性不能通过进一步的线性变换来消除。
Simoncelli & Schwartz (1999) 表明，这些依赖关系可以通过非线性处理消除，其中每个基函数的线性响应被校正（通常是平方），然后除以相邻神经元校正响应的加权和。许多作者使用类似的“除法归一化”模型来解释神经元中的非线性行为（Reichhardt & Poggio 1973、Bonds 1989、Geisler & Albrecht 1992、Heeger 1992、Carandini et al 1997）。因此，皮质处理中发现的非线性类型与自然图像的非高斯统计数据非常匹配。此外，可以选择用于计算归一化信号的权重以最大化归一化响应的独立性。所得到的模型出人意料地擅长解释各种神经生理学观察，在这些观察中，反应受到非最佳刺激的抑制，无论是在经典受体场内还是在外部（Simoncelli & Schwartz 1999，Wainwright 等人 2001）。定向滤波器响应之间的统计依赖性至少部分归因于自然图像中扩展轮廓的普遍性。Geisler 等人（2001）研究了附近位置的主导方向的经验分布，并使用它们来预测轮廓检测任务中的心理物理表现。Sigman 等人（2001）表明这些分布与共圆定向元素一致，并将这一结果与初级视觉皮层神经元的连接性联系起来。
时空统计
全面考虑图像统计及其与视觉系统中编码的关系时，时间因素必不可少。落在视网膜上的图像具有重要的时间结构，这些结构源自观察者的自身运动以及世界中物体的运动。此外，神经元具有重要的时间响应特性，在许多情况下，尚不清楚这些特性是否可以与其空间特性完全区分开来。然而，自然图像中时空统计的测量比空间统计要困难得多，因为获得逼真的时变视网膜图像需要在动物与世界互动时跟踪眼睛、头部和身体的运动。尽管如此，一些合理的近似值可以让人得出有用的见解。
与静态图像一样，表征联合时空统计的一个良好起点是自相关函数。在这种情况下，时空自相关函数 \(C(\Delta x,\Delta y,\Delta t)\) 将图像像素的成对相关性表征为其相对空间分离 \((\Delta x,\Delta y)\) 和时间分离 \(\Delta t\) 的函数。同样，假设时空平移不变性，我们发现该函数最方便在频域中表征。
表征时空功率谱的问题最早是由 van Hateren (1992) 间接研究的，他假设了一定的图像速度分布和 \(1/f^2\) 空间功率谱，并从中推断出联合时空谱，假设空间功率谱为 \(1/f^2\)。基于推断出的功率谱，van Hateren 随后计算出最佳神经滤波器，以最有效地利用后受体神经元的有限通道容量（类似于 Atick 的白化滤波器）。他从这一分析中表明，最佳神经滤波器与不同空间频带中大单极细胞的时间响应特性非常吻合。他还能够将这种分析扩展到人类视觉，以解释时空对比敏感度函数（van Hateren 1993）。
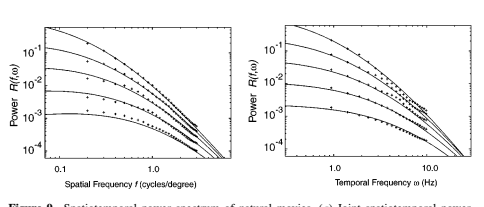
Dong 和 Atick (1995a) 通过计算许多短片片段（每个片段大约 2-4 秒长）的三维傅里叶变换并计算它们的功率谱平均值，直接估计了自然图像的时空功率谱。这种方法适用于一组商业电影以及作者制作的视频。他们的结果（如 Figure 9 所示）显示了空间频率和时间频率之间有趣的依赖关系。空间频率功率谱的斜率在较高的时间频率下变得更平缓。时间频率谱也是如此 - 即斜率在较高的空间频率下变得更平缓。Dong 和 Atick (1995a) 表明，空间频率和时间频率之间的这种相互依赖性可以通过假设物体运动的特定分布（即幂律分布）来解释，其形式类似于 van Hateren 的假设。通过再次应用白化原理，Dong & Atick（1995b）计算出了用于消除时间相关性的最佳时间滤波器，并表明它与从猫的外侧膝状体神经元测得的频率响应函数紧密匹配（在低空间频率下）。
尽管上述例子中理论与实验的匹配令人鼓舞，但它仍然没有回答视觉神经元在处理自然图像时是否表现如预期的问题。Dan 等人 (1996) 直接解决了这个问题，他们测量了麻醉猫对自然电影的反应中 LGN 神经元活动的时间频谱。与白化概念一致，响应电影的细胞输出功率相当平坦，作为时间频率的函数。相反，如果播放高斯白噪声电影，其中输入频谱是平坦的，LGN 细胞的输出频谱会随频率线性增加，这与神经元的时间频率响应特性相对应。因此，LGN 神经元通常不会白化任何刺激，只会白化那些表现出与自然图像相同的相关结构的刺激。
自然图像中时空结构的分析也可以扩展到高阶统计（超出自相关函数），如先前针对静态图像所述。van Hateren 和 Ruderman (1998) 最近进行了此类分析，他们将 ICA 算法应用于从电影中提取的许多局部图像块（12 × 12 像素乘以 12 帧时间）的集合。他们表明，从这种分析中得出的成分类似于 V1 神经元的方向选择性受体场 - 即它们在空间和时间上定位（在 12 × 12 × 12 窗口内）、空间定向和方向选择性（参见 Figure 10 ）。此外，使用学习到的受体场过滤图像产生的输出信号具有正峰度，这表明时变自然图像也可以用稀疏代码有效地描述，其中相对较少的神经元在空间和时间上都处于活动状态。 Lewick & Sejnowski (1999) 和 Olshausen (2001) 已证明这些输出信号可能高度稀疏，从而产生类似于神经脉冲序列的短暂、点状事件。
讨论
尽管有效编码假设早在四十多年前就被提出，但直到最近才开始对其进行定量研究。在理论方面，图像模型才刚刚开始具备足够的能力来做出有趣的预测。在实验方面，刺激生成和神经记录（尤其是多单元记录）的技术已经发展到可以测试理论预测的可行和实用的程度。下面，我们将讨论本综述中提出的想法的一些弱点和缺点，以及我们对图像统计知识的不断增长所带来的一些令人兴奋的新机遇。
高效编码假设最严重的缺陷在于它忽略了视觉系统的另外两个主要约束：实施和任务。一些作者成功地将实施约束与环境约束融合在一起（例如 Baddeley 等人 1998 年）。这些约束通常很难指定，但显然它们在整个大脑中发挥着重要作用。生物体面临的任务可能是一个更重要的约束。特别是，该假设仅指出信息必须有效地表示；它没有说明应该表示什么信息。许多作者认为，在处理的最早阶段（例如视网膜和 V1），系统最好提供一种通用图像表示，以尽可能多地保留有关传入信号的信息。事实上，高效编码原理在解释视网膜、LGN 和 V1 中神经元的响应特性方面的成功可以看作是对这一假设的验证。但最终，需要一个更丰富的理论框架。这种框架的一个常见示例是贝叶斯决策/估计理论，它既包括环境的先验统计模型，也包括损失或奖励函数，该函数指定不同错误的成本或不同行为的可取性。这些概念已广泛应用于感知（例如 Knill & Richards 1996），也已考虑用于神经表征（例如 Oram 等人 1998）。
有效编码假设的另一个重要问题是环境统计数据影响感觉系统的时间尺度。这个时间尺度可以是几千年（进化）、几个月（神经发育）或几分钟或几秒（短期适应）。本综述中讨论的大多数研究都假设系统是固定的，但直观上看，计算应该与相关时间尺度上的各种统计属性相匹配。例如，1/f2 功率谱属性是稳定的，因此需要一个在进化时间尺度上硬连线的解决方案。另一方面，最近的一些结果表明，单个神经元在非常短的时间尺度上适应对比度和空间尺度（Smirnakis 等人 1997 年）、方向（Muller 等人 1999 年）和方差（Brenner 等人 2000 年）的变化。在关节反应特性方面，Barlow & Foldiak（1989）提出短期适应作用可减少神经元之间的依赖性，最近已在心理物理学（例如 Atick 等人 1993 年、Dong 1995 年、Webster 1996 年、Wainwright 1999 年）和生理学（例如 Carandini 等人 1998 年、Dragoi 等人 2000 年、Wainwright 等人 2001 年）上发现了这一假设的证据。
除了预测神经元的响应特性之外，高效编码模型的潜在应用在于生成符合自然图像统计的视觉刺激。从历史上看，视觉神经元的特征是使用相当简单的测试刺激（例如条、光栅或斑点），这些刺激易于参数化和控制，并且能够引起剧烈的反应。但不能保证使用这种简单的测试刺激测量的反应可用于预测对自然场景的神经反应。另一方面，真正自然的刺激更难控制。一个有趣的可能性在于统计纹理建模，它已被用作理解人类视觉的工具（例如 Julesz 1962、Bergen & Adelson 1986）。Knill 等人（1990）和 Parraga 等人（1999）表明，人类在特定辨别任务上的表现对于具有自然二阶（即 1/f2）统计的纹理最好，而对于不太自然的图像则下降。一些最近的自然纹理统计模型提供了生成具有自然图像的一些高阶统计结构特征的人工图像的可能性（例如 Heeger & Bergen 1995、Zhu et al 1998、Portilla & Simoncelli 2000）。
我们在本综述中讨论的大多数模型都可以用单级神经网络来描述。例如，白化可以通过一组输入（光感受器）和输出（视网膜神经节细胞）之间的一组连接来实现。同样，稀疏编码和 ICA 模型可以通过 LGN 和皮质之间的连接来实现。但接下来是什么呢？我们能否尝试使用多阶段高效编码来模拟视觉区域 V2、V4、MT 或 MST 中神经元的功能？特别是，视觉皮层的结构表明了一种层次化组织，其中神经元对图像结构中越来越复杂的方面有选择性。原则上，这可以允许明确表示结构，例如曲率、表面甚至整个物体（例如 Dayan 等人 1995 年，Rao & Ballard 1997 年），从而为探索纹外皮层神经元的响应特性提供了原则基础。
虽然本综述主要关注视觉领域的发现，但其他感官信号也适用于统计分析。例如，Attias & Schreiner (1997) 已表明，许多自然声音在其功率谱中服从某种程度的自相似性，类似于自然图像。此外，M S Lewicki（个人通信）发现自然声音的独立成分类似于通常用于模拟听觉神经中神经元反应的“Gammatone”滤波器。Schwartz & Simoncelli (2001) 已表明，此类滤波器响应的除法归一化可用作自然声音的非线性白化操作，类似于视觉的情况。在使用自然声音作为实验刺激时，Rieke 等人 (1995) 已表明，青蛙听觉系统早期的神经元专门适应编码动物自然发声的结构。 Attias & Schreiner (1998) 证明，猫听觉中脑神经元对于自然刺激的信息传输率更高。
总体而言，我们认为最近在探索和测试环境统计数据与感觉之间的关系方面取得的进展令人鼓舞。迄今为止的结果主要是对神经功能的事后解释，而不是预测尚未观察到的感觉处理方面。但我们相信，这条研究路线最终会带来新的见解，并将有助于指导我们探索更高层次视觉领域的思维。
致谢
作者感谢 Horace Barlow 和 Matteo Carandini 的有益评论。EPS 得到了 Alfred P. Sloan 研究奖学金、NSF CA-REER 拨款 MIP-9796040、纽约大学斯隆理论神经生物学中心和霍华德休斯医学研究所的支持。BAO 得到了 NIMH R29-MH57921 的支持。
Visit The Annual Reviews Home Page At Www.Annualreviews.Org
引用文献
Atick JJ. 1992. Could information theory provide an ecological theory of sensory processing? Netw. Comput. Neural Syst. 3:213–51
Atick JJ, Li Z, Redlich AN. 1993. What does Rep. IASSNS-HEP-91/40, Inst. Adv. Study, Princeton, NJ
Atick JJ, Redlich AN. 1992. What does the retina know about natural scenes? Neural Comput. 4:196–210
Attias H, Schreiner CE. 1997. Temporal low-order statistics of natural sounds. In Advances in Neural Information Processing Systems, ed. MC Mozer, M Jordan, M Kearns, S Solla, 9:27–33. Cambridge, MA: MIT Press
Attias H. 1998. Independent factor analysis. Neural Comput. 11:803–51
Attias H, Schreiner CE. 1998. Coding of naturalistic stimuli by auditory midbrain neurons. In Advances in Neural Information Processing Systems , ed. M Jordan, M Kearns, S Solla, 10:103–9. Cambridge, MA: MIT Press.
Attneave F. 1954. Some informational aspects of visual perception. Psychol. Rev. 61:183–93
Baddeley R, Abbott LF, Booth MC, Sengpiel F, Freeman T, et al. 1998. Respones of neurons in primary and inferior temporal visual cortices to natural scenes. Proc. R. Soc. London Ser. B 264:1775–83
Balboa RM, Grzywacz NM. 2000. The role of early lateral inhibition: more than maximizing luminance information. Vīs. Res. 17:77–89
Barlow HB. 1961. Possible principles underlying the transformation of sensory messages. In Sensory Communication , ed. WA Rosenblith, pp. 217–34. Cambridge, MA: MIT Press
Barlow HB, Foldiak P. 1989. Adaptation and decorrelation in the cortex. In The Computing Neuron , ed. R Durbin, C Miall, G Mitchinson, 4:54–72. New York: Addison-Wellesley
Bell AJ, Sejnowski TJ. 1997. The “independent components” of natural scenes are edge filters. Vīs. Res. 37(23):3327–38
Bergen JR, Adelson EH. 1986. Visual texture segmentation based on energy measures. J. Opt. Soc. Am. A 3:99
Bialek W, Rieke F, de Ruyter van Steveninck RR, Warland D. 1991. Reading a neural code. Science 252:1854 - 57.
Bonds AB. 1989. Role of inhibition in the speci cation of orientation selectivity of cells in the cat striate cortex. Vis. Neurosci. 2:41–55
Brenner N, Bialek W, de Ruyter van Steveninck RR. 2000. Adaptive rescaling maximizes information transmission. Neuron 26:695–702
Buccigrossi RW, Simoncelli EP. 1999. Image compression via joint statistical characterization in the wavelet domain. IEEE Trans. Image Proc. 8(12):1688–701.
Buchsbaum G, Gottschalk A. 1983. Trichromacy, opponent color coding, and optimum colour information transmission in the retina. Proc. R. Soc. London Ser. B 220:89–113
Buchsbaum G, Gottschalk A. 1984. Chromaticity coordinates of frequency-limited functions. J. Opt. Soc. Am. A 1(8):885–87 .
Carandini M, Heeger DJ, Movshon JA. 1997. Linearity and normalization in simple cells of the macaque primary visual cortex. J. Neurosci. 17:8621–44.
Carandini M, Movshon JA, Ferster D. 1998. Pattern adaptation and cross-orientation interactions in the primary visual cortex. Neuropharmacology 37:501–11
Cardoso JF. 1989. Source separation using higer order moments. In Int. Conf. Acoustics Speech Signal Proc. , pp. 2109–12. IEEE Signal Process. Soc.
Common P. 1994. Independent component analysis, a new concept? Signal Process 36:387–14
Dan Y, Atick JJ, Reid RC. 1996. Efficient coding of natural scenes in the lateral geniculate nucleus: experimental test of a computational theory. J. Neurosci. 16:3351–62
Daugman JG. 1989. Entropy reduction and decorrelation in visual coding by oriented neural receptive fields. IEEE Trans. Biomed. Eng. 36(1):107–14.
Dayan P, Hinton GE, Neal RM, Zemel RS.1995. The Helmholtz machine. Neural Comput. 7:889–904.
Dong DW. 1995. Associative decorrelation dynamics: a theory of self-organization and optimization in feedback networks. In Advances in Neural Information Processing Systems , ed. G Tesauro, D Touretzky, T Leen. 7:925–32
Dong DW, Atick JJ. 1995a. Statistics of natural time-varying images. Netw. Comput. Neural Syst. 6:345–58.
Dong DW, Atick JJ. 1995b. Temporal decorrelation: a theory of lagged and nonlagged responses in the lateral geniculate nucleus. Netw. Comput. Neural Syst. 6:159–78
Dragoi V, Sharma J, Sur M. 2000. Adaptationinduced plasticity of orientation tuning in adult visual cortex. Neuron 28:287–88
Field DJ. 1987. Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 4(12):2379–94.
Field DJ. 1994. What is the goal of sensory coding? Neural Comput. 6:559–601.
Foldiak P. 1990. Forming sparse representations by local anti-hebbian learning. Biol. Cybernet. 64:165–70
Geisler WS, Albrecht DG. 1992. Cortical neurons: isolation of contrast gain control. Vis. Res. 8:1409–10
Geisler WS, Perry JS, Super BJ, Gallogly DP. 2001. Edge co-occurance in natural images predicts contour grouping performance. Vis. Res. 41:711–24.
Hancock PJB, Baddeley RJ, Smith LS. 1992. The principal components of natural images. Network 3:61–72
Heeger D, Bergen J. 1995. Pyramid-based texture analysis/synthesis. In Proc. Assoc. Comput. Mach. Special Interest Groups Graph , p. 229–38
Heeger DJ. 1992. Normalization of cell responses in cat striate cortex. Vis. Neurosci. 9:181–98
Hyvärinen A, Hoyer P. 2000. Emergence of topography and complex cell properties from natural images using extensions of ica. In Advances in Neural Information Processing Systems , ed. SA Solla, TK Leen, K-R Müller, 12:827–33, Cambridge, MA: MIT Press
Hyvärinen A, Oja E. 1997. A fast fixed-point algorithm for independent component analysis. Neural Comput. 9:1483–92.
Jaynes ET. 1978. Where do we stand on maximum entropy? In The Maximal Entropy Formalism , ed. RD Levine, M Tribus, pp. 620–30. Cambridge, MA: MIT Press
Julesz B. 1962. Visual pattern discrimination. IRE Trans. Inf. Theory , IT-8
Jutten C, Herault J. 1991. Blind separation of sources. Part I: An adaptive algorithm based on neuromimetic architecture. Signal Process 24(1):1–10 Kersten D. 1987. Predictability and redundancy of natural images. J. Opt. Soc. Am. A 4(12):2395–400
Knill DC, Field D, Kersten D. 1990. Human discrimination of fractal images. J. Opt. Soc. Am. A 7:1113–23
Knill DC, Richards W, eds. 1996. Perception as Bayesian Inference . Cambridge, UK: Cambridge Univ. Press Laughlin SB. 1981. A simple coding procedure enhances a neuron’s information capacity. Z. Naturforsch. 36C:910–12.
Lee AB, Mumford D. 1999. An occlusion model generating scale-invariant images. In IEEE Workshop on Statistical and Computational Theories of Vision , Fort Collins, CO. Also at http://www.cis.ohiostate.edu/~szhu/ SCTV99.html
Lennie P, D’Zmura M. 1988. Mechanisms of color vision. CRC Crit. Rev. Neurobiol. 3:33–400
Lewicki MS, Olshausen BA. 1999. Probabilistic framework for the adaptation and comparison of image codes. J. Opt. Soc. Am. A 16(7):1587–601
Lewicki M, Sejnowski T. 1999. Coding timevarying signals using sparse, shift-invariant representations. In Advances in Neural Information Processing Systems , ed. MS Kearns, SA Solla, DA Cohn, 11:815–21. Cambridge, MA: MIT Press
Maloney LT. 1986. Evaluation of linear models of surface spectral reflectance with small numbers of parameters. J. Opt. Soc. Am. A3(10):1673–83
Müller JR, Metha AB, Krauskopf J, Lennie P. 1999. Rapid adaptation in visual cortex to the structure of images. Science 285:1405–8
Olshausen BA. 2001. Sparse codes and spikes. In Statistical Theories of the Brain , ed. R Rao, B Olshausen, M Lewicki. Cambridge, MA: MT Press. In press
Olshausen BA, Field DJ. 1996. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 381:607–9
Olshausen BA, Field DJ. 1997. Sparse coding with an overcomplete basis set: a strategy employed by V1? Vis. Res. 37:3311–25
Oram MW, Foldiak P, Perrett DI, Sengpiel F. 1998. The “ideal homunculus”: decoding neural population signals. Trends Neurosci . 21(6):259–65
Parraga CA, Troscianko T, Tolhurst DJ. 2000. The human visual system is optimised for processing the spatial information in natural visual images. Curr. Biol. 10:35–38
Penev P, Gegiu M, Kaplan E. 2000. Fast convergent factorial learning of the lowdimensional independent manifolds in optical imaging data. In Proc. 2nd Int. Workshop Indep. Comp. Anal. Signal Separation, pp. 133–38.
Helsinki, Finland Portilla J, Simoncelli EP. 2000. A parametric texture model based on joint statistics of complex wavelet coefficients. Int. J. Comput. Vīs.40(1):49–71.
Rao RPN, Ballard DH. 1997. Dynamic model of visual recognition predicts neural response properties in the visual cortex. Neural Comput. 9:721–63
Reichhardt W, Poggio T. 1979. Figure-ground discrimination by relative movement in the visual system of the fly. Biol. Cybernet.35:81–100
Reinagel P, Zador AM. 1999. Natural scene statistics at the centre of gaze. Netw. Comput. Neural Syst. 10:341–50.
Rieke F, Bodnar DA, Bialek W. 1995. Naturalistic stimuli increase the rate and efficiency of information transmission by primary auditory afferents. Proc. R. Soc. London B 262:259–65
Ruderman DL. 1997. Origins of scaling in natural images. Vīs. Res. 37:3385–98
Ruderman DL, Bialek W. 1994. Statistics of natural images: scaling in the woods. Phys. Rev. Lett. 73(6):814–17
Ruderman DL, Cronin TW, Chiao CC. 1998. Statistics of cone responses to natural images: implications for visual coding. J. Opt. Soc. Am. A 15(8):2036–45.
Sanger TD. 1989. Optimal unsupervised learning in a single-layer network. Neural Netw. 2:459–73
Schwartz O, Simoncelli E. 2001. Natural sound statistics and divisive normalization in the auditory system. In Advances in Neural Information Processing Systems , ed. TK Leen, TG Dietterich, V Tresp, Vol. 13. Cambridge, MA: MIT Press. In Press
Shannon C. 1948. The mathematical theory of communication. Bell Syst. Tech. J. 27:379–424
Shouval H, Intrator N, Cooper LN. 1997. BCM Network develops orientation selectivity and ocular dominance in natural scene environment. Vis. Res. 37(23):339–42
Sigman M, Cecchi GA, Gilbert CD, Magnasco MO. 2001. On a common circle: natural scenes and gestalt rules. Proc. Natl. Acad. Sci. 98(4):1935–40.
Simoncelli EP. 1997. Statistical Models for Images: Compression , Restoration and Synthesis . Asilomar Conf. Signals, Systems, Comput. 673–78. Los Alamitos, CA: IEEE Comput. Soc. http://www.cns.nyu.edu/~eero/publications.html
Simoncelli EP, Schwartz O. 1999. Image statistics and cortical normalization models. In Advances in Neural Information Processing Systems , ed. MS Kearns, SA Solla, DA Cohn. 11:153–59
Smirnakis SM, Berry MJ, Warland DK, Bialek W, Meister M. 1997. Adaptation of retinal processing to image contrast and spatial scale. Nature 386:69–73 Srinivasan MV, Laughlin SB, Dubs A. 1982.
Predictive coding: A fresh view of inhibition in the retina. J. R. Soc. London Ser. B 216:427–59.
van Hateren JH. 1992. A theory of maximizing sensory information. Biol. Cybern. 68:23–29
van Hateren JH. 1993. Spatiotemporal contrast sensitivity of early vision. Vis. Res. 33:257–67
van Hateren JH, van der Schaaf A. 1998. Independent component fi lters of natural images compared with simple cells in primary visual cortex. Proc. R. Soc. London Ser. B 265:359–666
Vinje WE, Gallant JL. 2000. Sparse coding and decorrelation in primary visual cortex during natural vision. Science 287:1273–76
Wainwright MJ. 1999. Visual adaptation as optimal information transmission. Vīs. Res.39:3960–74.
Wainwright MJ, Schwartz O, Simoncelli EP. 2001. Natural image statistics and divisive normalization: modeling nonlinearity and adaptation in cortical neurons. In Statistical Theories of the Brain , ed. R Rao, B Olshausen, M Lewicki. Cambridge, MA: MIT Press. In press
Webster MA. 1996. Human colour perception and its adaptation. Netw. Comput. Neural Syst. 7:587–634.
Wegmann B, Zetzsche C. 1990. Statistical dependence between orientation filter outputs used in an human vision based image code. In Proc. SPIE Vis. Commun. Image Processing, 1360:909–22. Lausanne, Switzerland: Soc. Photo-Opt. Instrum. Eng.
Zhu SC, Wu YN, Mumford D. 1998. FRAME: Filters, random fields and maximum entropy—towards a unified theory for texture modeling. Int. J. Comp. Vis. 27(2):1–11, 120
Footnotes
暂时，我们认为响应是一个瞬时标量值。例如，这可能是膜电位或瞬时放电率↩︎
更一般地，考虑形式为 \(\varepsilon[\phi(x)]=c\) 的约束，其中 x 是响应，\(\phi\) 是约束函数，\(\varepsilon\) 表示对给定输入集合的响应的预期值或平均值，\(c\) 是常数。最大信息响应分布 [也称为最大熵分布 (Jaynes 1978)] 是 \(\mathcal{P}(x)\propto e^{-\lambda\phi(x)}\)，其中 \(\lambda\) 是常数。↩︎
可以使用标准线性代数技术计算这些轴：它们与数据协方差矩阵的特征向量相对应。↩︎
多维高斯密度是标量高斯密度向矢量的简单扩展。具体来说，密度的形式是 \(\mathcal{P}(\vec{x})\propto\exp[-\vec{x}^{T}\Lambda^{-1}\vec{x}/2]\) ，其中 \(\text{Λ}\) 是协方差矩阵。该密度的所有边际密度和条件密度也都是高斯分布。↩︎
线性代数上，这三个操作（旋转-缩放-旋转）直接对应于混合矩阵的奇异值分解。↩︎
从数据中盲目恢复独立源的问题仍然是一个活跃的研究领域（例如 Hyvarinen & Oja 1997、Attias 1998、Penev et al 2000）。↩︎
Reinagel & Zador (1999) 记录了人类观察者观看自然图像时的眼睛位置，发现这些位置附近的相关性强度下降得比一般位置更快。↩︎